6. ЭЛЕКТРОСТАТИКА ДИЭЛЕКТРИКОВ.
Теорема
единственности для решения граничных задач электростатики диэлектриков.
Потенциал точечного заряда в присутствии диэлектрического полупространства.
Диэлектрический шар в однородном электрическом поле. Потенциал распределенных
зарядов. Полярные и неполярные молекулы в диэлектрике. Поляризация плотных
неполярных диэлектриков. Формулы Клаузиуса![]() –
Моссотти и Лоренца. Поляризация полярных диэлектриков.
–
Моссотти и Лоренца. Поляризация полярных диэлектриков.
6.1.
Теорема единственности для решения граничных задач электростатики диэлектриков.
Докажем единственность решения задачи
о потенциале в среде, состоящей из некоторого числа диэлектриков с постоянными
диэлектрическими проницаемостями ![]() (Рис. 6.1). В каждой
из областей потенциал удовлетворяет уравнению Пуассона
(Рис. 6.1). В каждой
из областей потенциал удовлетворяет уравнению Пуассона
![]() , (6.1)
, (6.1)
где
![]() - плотность зарядов на границе
- плотность зарядов на границе ![]() - го диэлектрика с проводниками,
- го диэлектрика с проводниками, ![]() - плотность сторонних зарядов в области
- плотность сторонних зарядов в области ![]() . На границе раздела сред
. На границе раздела сред ![]() должны выполняться граничные условия
должны выполняться граничные условия
![]() , (6.2)
, (6.2)
где
![]() - плотность поверхностного заряда. Так как
- плотность поверхностного заряда. Так как
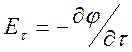 , то первое из условий (6.2) будет
выполнено, если на границе раздела сред
, то первое из условий (6.2) будет
выполнено, если на границе раздела сред ![]() выполнено
условие
выполнено
условие
![]() . (6.3)
. (6.3)
Второе условие в (6.2) перейдет в следующее
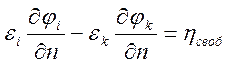 . (6.4)
. (6.4)
Таким
образом, задача электростатики диэлектриков сводится к решению уравнения (6.1)
с известными функциями ![]() с учетом граничных
условий (6.3), (6.4). Утверждается, что решение такой задачи единственно,
потенциал
с учетом граничных
условий (6.3), (6.4). Утверждается, что решение такой задачи единственно,
потенциал ![]() находится с точностью до постоянного
слагаемого. Последнее не влияет на электрическое поле, так как
находится с точностью до постоянного
слагаемого. Последнее не влияет на электрическое поле, так как ![]() Доказательство проводится от противного.
Пусть
Доказательство проводится от противного.
Пусть ![]() и
и ![]() - два
различных решения задачи, причем
- два
различных решения задачи, причем ![]() . Так как
. Так как ![]() и
и ![]() удовлетворяют
уравнению (6.1) с одними и теми же источниками, то
удовлетворяют
уравнению (6.1) с одними и теми же источниками, то ![]() . На
границах
. На
границах ![]() потенциал будет удовлетворять условиям
потенциал будет удовлетворять условиям
![]() ,
, 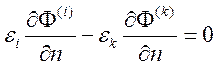 . (6.5)
. (6.5)
Воспользуемся формулой Грина
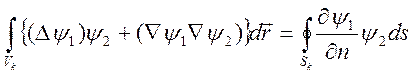 .
.
где
![]() - замкнутая поверхность, охватывающая
объем
- замкнутая поверхность, охватывающая
объем ![]() , занимаемый диэлектриком с проницаемостью
, занимаемый диэлектриком с проницаемостью ![]() ,
, ![]() -
внешняя по отношению к
-
внешняя по отношению к ![]() нормаль на поверхности
нормаль на поверхности ![]() . Возьмем
. Возьмем ![]() .
Формула Грина с учетом однородного уравнения Пуассона для
.
Формула Грина с учетом однородного уравнения Пуассона для ![]() и суммирования по
и суммирования по ![]() дает.
дает. 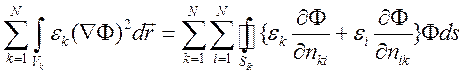 (6.6)
(6.6)
При написании этого соотношения
учтено, что интегрирование по поверхности ![]() возникает
дважды: один раз, когда формула Грина пишется для объема
возникает
дважды: один раз, когда формула Грина пишется для объема ![]() с диэлектриком
с диэлектриком ![]() , а
другой раз, для соседнего объема
, а
другой раз, для соседнего объема ![]() с диэлектриком
с диэлектриком ![]() . Нормали обладают свойством
. Нормали обладают свойством ![]() . С учетом этого свойства и второго
граничного условия в (6.5) правая часть в (6.6) обращается в ноль. Имеем
. С учетом этого свойства и второго
граничного условия в (6.5) правая часть в (6.6) обращается в ноль. Имеем
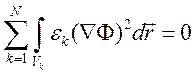 .
.
Так как ![]() ,
то из равенства интеграла нулю следует, что
,
то из равенства интеграла нулю следует, что
![]() ,
,
а это означает единственность решения рассматриваемой задачи.
6.2. Потенциал точечного заряда в присутствии диэлектрического полупространства. Смещение зарядов в молекулах однородного безграничного изотропного диэлектрика, помещенного в электростатическое поле, приводит к уменьшению результирующего поля в диэлектрике. Если диэлектрик ограничен, то изменение поля не сводится к масштабному уменьшению. Как правило, происходит существенное изменение пространственной структуры поля. При решении таких задач используется принцип единственности задач электростатики. Если с помощью суперпозиции электростатических полей удается удовлетворить граничным условиям на поверхности диэлектрика, то эта суперпозиция представляет собой истинное поле.
Определим
потенциал, создаваемый точечным зарядом ![]() в
присутствии диэлектрического полупространства с плоской границей (Рис. 6.2).
Используем метод изображений. При этом идея использования фиктивных зарядов
(изображений) несколько отличается от идеи изображений в задачах электростатики
проводников (раздел 5.6). Считаем, что напряженность поля в вакууме будет таким
же, как в отсутствии диэлектрика, но при наличии зеркального (фиктивного
заряда)
в
присутствии диэлектрического полупространства с плоской границей (Рис. 6.2).
Используем метод изображений. При этом идея использования фиктивных зарядов
(изображений) несколько отличается от идеи изображений в задачах электростатики
проводников (раздел 5.6). Считаем, что напряженность поля в вакууме будет таким
же, как в отсутствии диэлектрика, но при наличии зеркального (фиктивного
заряда) ![]() . Этот заряд помещается в точку
. Этот заряд помещается в точку ![]() в диэлектрике. Относительная диэлектрическая
проницаемость этого диэлектрика
в диэлектрике. Относительная диэлектрическая
проницаемость этого диэлектрика ![]() . Реальный заряд
. Реальный заряд ![]() находится в вакууме в точке
находится в вакууме в точке ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.