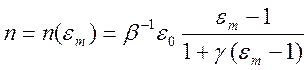Электростатика диэлектриков. Теорема единственности для решения граничных задач электростатики диэлектриков. Потенциал точечного заряда в присутствии диэлектрического полупространства, страница 4

                                    .

Экспериментальные исследования показывают, что . Если взять , то получим известную формулу Клаузиуса – Моссотти

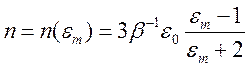                                    ,                             (6.14)

дополнительно из (6.13) получается формула Лоренца

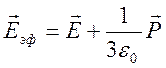                                                .                               (6.15)

Соотношение (6.13) принимает вид

                                                .

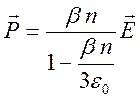С учетом (6.14) и (6.15) получаем выражение

                                                ,

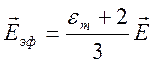Если молекулу в диэлектрике удалить и на ее месте сделать сферическую вакуумную полость, то представление для  в таком приближении дается формулой (6.10), где под  следует понимать среднее по пространству поле

                                                .                                

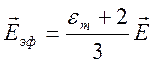Это подтверждает возможность моделирования неполярной молекулы сферической вакуумной полостью.

6.7. Поляризация полярных диэлектриков. Рассмотрим теперь газ, состоящий из одинаковых полярных молекул. Электрическое поле стремится ориентировать собственные дипольные моменты молекул по полю. Этой тенденции препятствует тепловое движение молекул. При отсутствии внешнего поля  дипольные моменты ориентированы хаотически, все направления  равновероятны, поэтому вектор поляризации в таком состоянии .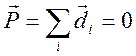

            При  внешне поле создает преимущественное направление для ориентации при суммировании этих моментов необходимо учитывать вероятность распределения диполей по разным направлениям дипольных моментов . Модуль полного дипольного момента единичного сферического объема в этом случае будет определяться по формуле

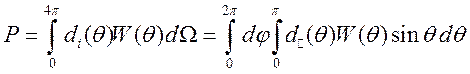,     ,            (6.16)

где  - угол между векторами  и 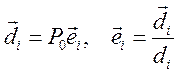. Угол  является полярным углом в выбранной сферической системе координат,  - элемент телесного угла,  - азимутальный угол,  - функция плотности вероятности распределения дипольных моментов  по углам ,  - параллельная внешнему полю составляющая дипольного момента молекулы.

            Перпендикулярные внешнему полю составляющие дипольных моментов молекул из-за их равновероятного распределения по углу  не дают вклада в полный дипольный момент объема.

            Если молекулы находятся в состоянии статистического равновесия, то функция плотности вероятности определяется формулой Больцмана

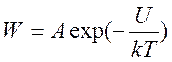                                                ,                                          (6.16а)

где  - нормировочный множитель,  - постоянная Больцмана,  - температура,  - потенциальная энергия полярной молекулы во внешнем поле, она минимальна при  и она максимальна при . Нелинейная зависимость (6.16а) приводит к возникновению нелинейной связи . Это соответствует учету нелинейных эффектов в электростатик полярных диэлектриков. В результате имеем

                                                .

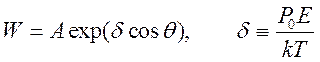Нормировочный множитель находится из условия

                                                ,

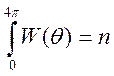где  -концентрация молекул. Получаем уравнение для определения

                                    .

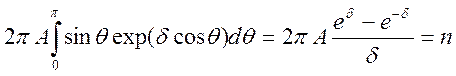Для определения вектора поляризации в формуле (6.16) необходимо вычислить интеграл

.

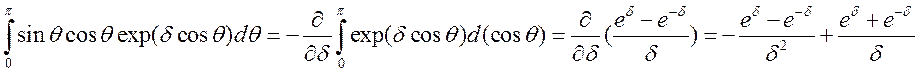Получается представление для абсолютной величины вектора поляризации

                                                ,                                                  (6.17)

где  - функция Ланжевена,

                        .

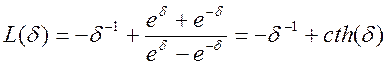Направление вектора поляризации совпадает с направлением поля . Получим представление для вектора поляризации и для диэлектрической проницаемости в предельном случае слабого поля и большой энергии теплового движения молекул:

                                    ,          .

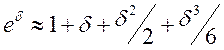При этом имеем ,       .

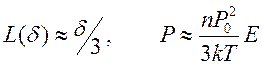Выражение для диэлектрической проницаемости получается из представления

                                    ,

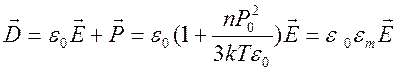откуда следует

                                                ,                      .

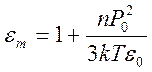Диэлектрическая проницаемость полярных диэлектриков в отличие от неполярных диэлектриков зависит от температуры. Поэтому если экспериментально установлена зависимость диэлектрической проницаемости от температуры, то это значит, что диэлектрик состоит из полярных молекул.

            Другая предельная ситуация соответствует сильному полю, когда наступает эффект насыщения (все диполи ориентированы по полю):

            ,                      ,            .

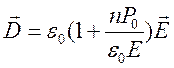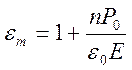Зависимость диэлектрической проницаемости полярного диэлектрика от поля  отражает нелинейный характер поляризуемости таких сред.