Далее, предполагаем, что поле в диэлектрике будет
таким же как и поле дополнительного фиктивного заряда ![]() в
неограниченном диэлектрике (без вакуумного полупространства) и расположенном в
точке
в
неограниченном диэлектрике (без вакуумного полупространства) и расположенном в
точке ![]() (это точка расположения реального заряда).
На Рис. 6.2
(это точка расположения реального заряда).
На Рис. 6.2 ![]() и
и ![]() - это
точки наблюдения соответственно в вакууме и в диэлектрике. Итак, предполагаем,
что потенциалы
- это
точки наблюдения соответственно в вакууме и в диэлектрике. Итак, предполагаем,
что потенциалы ![]() и
и ![]() в
вакууме и диэлектрике определяются формулами
в
вакууме и диэлектрике определяются формулами
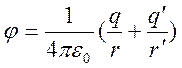 ,
, 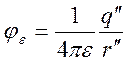 .
.
В
этих соотношениях имеются два неизвестных параметра ![]() и
и ![]() .Потенциалы
.Потенциалы ![]() и
и ![]() удовлетворяют уравнениям электростатики.
Эти представления будут давать решение задачи, если выполняются граничные
условия на поверхности диэлектрика. С этой целью подбираются величины пока еще
произвольных двух констант
удовлетворяют уравнениям электростатики.
Эти представления будут давать решение задачи, если выполняются граничные
условия на поверхности диэлектрика. С этой целью подбираются величины пока еще
произвольных двух констант ![]() и
и ![]() . Непрерывность тангенциальной составляющей
электрического поля эквивалентна непрерывности потенциала. На границе раздела
точки
. Непрерывность тангенциальной составляющей
электрического поля эквивалентна непрерывности потенциала. На границе раздела
точки ![]() и
и ![]() совпадают
и
совпадают
и ![]() . Непрерывность потенциала обеспечивается
выполнением условия
. Непрерывность потенциала обеспечивается
выполнением условия
![]() . (6.7)
. (6.7)
Второе
граничное условие это непрерывность нормальной составляющей вектора
электрической индукции ![]() . Для вектора электрической
индукции в двух полупространствах можно получить представления
. Для вектора электрической
индукции в двух полупространствах можно получить представления
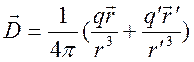 ,
, 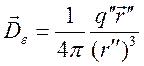 .
.
На
границе диэлектрика ![]() и из условия
и из условия ![]() получаем
получаем
![]() . (6.8)
. (6.8)
Из условий (6.7) и (6.8) находим искомые величины
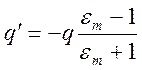 ,
, 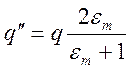 .
.
Теорема единственности обеспечивает истинность построенного решения.
6.3.
Диэлектрический шар в однородном электрическом поле. Рассмотрим задачу о модификации однородного
электростатического поля ![]() (Рис. 6.3) в которое
помещается диэлектрический шар радиуса
(Рис. 6.3) в которое
помещается диэлектрический шар радиуса ![]() с
диэлектрической проницаемостью
с
диэлектрической проницаемостью ![]() . Проницаемость
окружающей среды
. Проницаемость
окружающей среды ![]() . При внесении диэлектрического
объекта в однородное поле, поле внутри его, вообще говоря, становится
неоднородным. В этом отношении данная задача является «экзотической» - будет
показано, что поле внутри диэлектрического шара окажется однородным. Введем
сферическую систему координат, полярная ось которой проходит через центр шара
по направлению поля
. При внесении диэлектрического
объекта в однородное поле, поле внутри его, вообще говоря, становится
неоднородным. В этом отношении данная задача является «экзотической» - будет
показано, что поле внутри диэлектрического шара окажется однородным. Введем
сферическую систему координат, полярная ось которой проходит через центр шара
по направлению поля ![]() .Очевидно, что задача обладает
осевой симметрией, ее решение не зависит от азимутального угла. Потенциал во
внешней среде будем искать в виде суперпозиции
.Очевидно, что задача обладает
осевой симметрией, ее решение не зависит от азимутального угла. Потенциал во
внешней среде будем искать в виде суперпозиции
![]() ,
,
где
![]() - потенциал постоянного внешнего поля,
- потенциал постоянного внешнего поля, ![]() - потенциал, создаваемый шаром. Потенциал
внутри шара обозначим
- потенциал, создаваемый шаром. Потенциал
внутри шара обозначим ![]() . Свободные заряды в диэлектриках
отсутствуют, поэтому потенциалы
. Свободные заряды в диэлектриках
отсутствуют, поэтому потенциалы ![]() и
и ![]() удовлетворяют однородному уравнению
Пуассона. Общее решение этого уравнения можно представить (см. раздел 5.8.
«Метод разделения переменных») в виде разложения по полиномам Лежандра
удовлетворяют однородному уравнению
Пуассона. Общее решение этого уравнения можно представить (см. раздел 5.8.
«Метод разделения переменных») в виде разложения по полиномам Лежандра
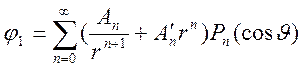 ,
, 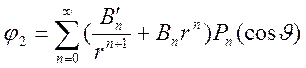 .
.
Потенциалы
![]() и
и ![]() должны
удовлетворять условиям конечности их величин:
должны
удовлетворять условиям конечности их величин:
![]() конечно при
конечно при ![]() ,
, ![]() конечно при
конечно при ![]() . Это
обеспечивается при
. Это
обеспечивается при ![]() . Получаем представления
. Получаем представления
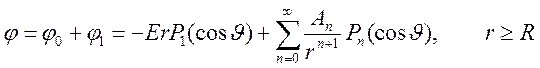 ,
,
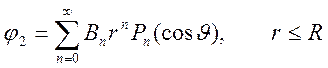 .
.
На
поверхности шара при ![]() эти потенциалы должны
удовлетворять условиям
эти потенциалы должны
удовлетворять условиям
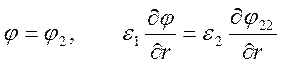 ,
,
вытекающим
из граничных условий для ![]() и
и ![]() . Приходим к уравнениям
. Приходим к уравнениям
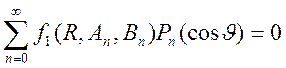 .
. 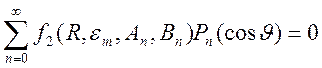 ,
, 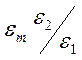 ,
,
из
которых в силу ортогональности полиномов Лежандра будем иметь систему двух
уравнений для определения ![]() и
и ![]()
![]()
![]() . (6.9)
. (6.9)
Непосредственной
проверкой можно убедиться, что эта система благодаря ортогональности полиномов
Лежандра,имеет ненулевое решение только при одном значении ![]() и (6.9) и принимает вид
и (6.9) и принимает вид
![]() ,
, ![]() .
.
Решение этой системы дает
 ,
, 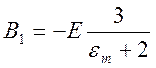 .
.
В
результате потенциал ![]() , описывающий возмущающее
действие диэлектрического шара в области
, описывающий возмущающее
действие диэлектрического шара в области ![]() имеет
вид потенциала диполя, помещенного в центр шара
имеет
вид потенциала диполя, помещенного в центр шара
 ,
,
где
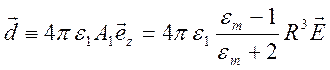 .
.
Для потенциала внутри шара имеем
![]()
и электрическое поле внутри шара представляется в виде
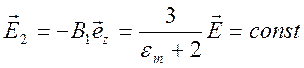 .
.
Таким
образом, если в однородное поле вносится диэлектрический шар, то поле в нем
однородно и отличается от внешнего поля в 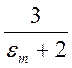 раз.
Возникает вопрос: при каких еще формах диэлектрика соблюдается это свойство?
Оказывается, что это будет для диэлектрика в форме эллипсоида и бесконечного
цилиндра, ось которого направлена вдоль внешнего поля. В отличие от
раз.
Возникает вопрос: при каких еще формах диэлектрика соблюдается это свойство?
Оказывается, что это будет для диэлектрика в форме эллипсоида и бесконечного
цилиндра, ось которого направлена вдоль внешнего поля. В отличие от ![]() , поле
, поле ![]() не
зависит от размера диэлектрического шара. При
не
зависит от размера диэлектрического шара. При ![]() имеем
имеем ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.