Так
как ![]() это поле в диэлектрическом шаре, то полю
это поле в диэлектрическом шаре, то полю ![]() можно придать смысл эффективного или
действующего поля
можно придать смысл эффективного или
действующего поля ![]() (поля, действующего на
диэлектрический шар, моделирующий молекулу, подробнее об этом будет сказано в
разделе 6.6)
(поля, действующего на
диэлектрический шар, моделирующий молекулу, подробнее об этом будет сказано в
разделе 6.6)
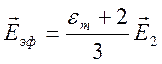 . (6.10)
. (6.10)
Формула (6.10) дает приближенное представление электростатического поля вдали от сферического диэлектрика.
6.4.
Потенциал распределенных зарядов. Уравнения
электростатики для случая распределенной плотности сторонних зарядов ![]() , имеют вид
, имеют вид
![]() .
.
Потенциал
![]() удовлетворяет уравнению Пуассона
удовлетворяет уравнению Пуассона
![]() .
.
В
случае точечного заряда ![]() и
и 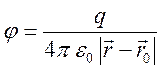 . Если
. Если ![]() -
непрерывная функция координат, то заряд
-
непрерывная функция координат, то заряд ![]() ,
сосредоточенный в бесконечно малом объеме
,
сосредоточенный в бесконечно малом объеме ![]() можно
считать точечным. Он создает потенциал
можно
считать точечным. Он создает потенциал
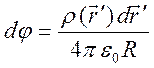 ,
,
где
![]() - расстояние от элемента
- расстояние от элемента ![]() до точки наблюдения
до точки наблюдения ![]() . Потенциал, создаваемый объемным распределением
зарядов
. Потенциал, создаваемый объемным распределением
зарядов ![]() и поверхностным распределением зарядов
и поверхностным распределением зарядов ![]() , получается как суперпозиция
соответствующих вкладов:
, получается как суперпозиция
соответствующих вкладов:
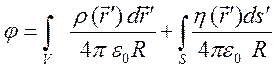 .
.
6.5.
Полярные и неполярные молекулы в диэлектрике. Уменьшение поля в диэлектрике по сравнению с вакуумом
(при тех же сторонних зарядах) связано со смещением зарядов в молекулах
диэлектрика под действием электрического поля. Такое смещение зарядов приводит
к возникновению у молекул направленного вдоль поля дипольного момента. При этом
следует различать два принципиально различных типа молекул. Молекула одного
типа (неполярные) сами по себе в отсутствии поля не обладают дипольным
моментом, но дипольный момент у них возникает под действием поля. Поле как бы
растягивает молекулу и раздвигает ее заряды. Положительные заряды смещаются по
полю, а отрицательные против поля. При не очень сильных полях (в линейном
приближении) дипольный момент неполярной молекулы ![]() оказывается
пропорциональным напряженности электрического поля:
оказывается
пропорциональным напряженности электрического поля: ![]() , где
, где ![]() - коэффициент поляризуем ости молекулы.
- коэффициент поляризуем ости молекулы.
Молекулы
другого типа (полярные) обладают собственным (спонтанным)
дипольным моментом ![]() при отсутствии внешнего поля.
Хотя молекулы полярного диэлектрика и обладают спонтанным дипольным моментом,
направления дипольных моментов отдельных молекул у полярных газов, жидкостей и
ряда твердых диэлектриков распределены в отсутствие поля хаотически. Поэтому
сумма дипольных моментов всех молекул в отсутствие поля равна нулю. Если
полярную молекулу поместить в электрическое поле
при отсутствии внешнего поля.
Хотя молекулы полярного диэлектрика и обладают спонтанным дипольным моментом,
направления дипольных моментов отдельных молекул у полярных газов, жидкостей и
ряда твердых диэлектриков распределены в отсутствие поля хаотически. Поэтому
сумма дипольных моментов всех молекул в отсутствие поля равна нулю. Если
полярную молекулу поместить в электрическое поле ![]() , то на
нее будет действовать пара сил с моментом
, то на
нее будет действовать пара сил с моментом ![]() . Эта
пара вращает диполь, стремясь расположить его вдоль поля. Таким образом,
действие поля в случае полярного диэлектрика является прежде всего
ориентирующим. Поле стремится ориентировать дипольные моменты отдельных молекул
вдоль поля. Конечно, полярные молекулы, так же как и неполярные молекулы, могут
деформироваться под действием внешнего поля. Однако, этот эффект является
второстепенным по сравнению с ориентационным.
. Эта
пара вращает диполь, стремясь расположить его вдоль поля. Таким образом,
действие поля в случае полярного диэлектрика является прежде всего
ориентирующим. Поле стремится ориентировать дипольные моменты отдельных молекул
вдоль поля. Конечно, полярные молекулы, так же как и неполярные молекулы, могут
деформироваться под действием внешнего поля. Однако, этот эффект является
второстепенным по сравнению с ориентационным.
6.6. Поляризация плотных неполярных диэлектриков. Формулы Клаузиуса – Моссотти и Лоренца. В разделе 6.5 при обсуждении свойств неполярных диэлектриков подразумевалось, что в формуле для дипольного момента отдельной молекулы
![]() ,
,
поле
![]() имеет смысл среднего по пространству поля.
имеет смысл среднего по пространству поля.
В случае полей малой амплитуды (линейное приближение), эту формулу можно представить в следующем альтернативном виде
![]() ,
,
где
![]() ,
, ![]() - эффективное
или действующее поле – поле действующее в той точке, где расположена
молекула (при этом предполагается что сама молекула из этой точки удалена).
Различие между
- эффективное
или действующее поле – поле действующее в той точке, где расположена
молекула (при этом предполагается что сама молекула из этой точки удалена).
Различие между ![]() и
и ![]() тем
больше, чем больше плотность частиц в диэлектрике.
тем
больше, чем больше плотность частиц в диэлектрике.
Суммарный дипольный момент единицы объема это вектор поляризации
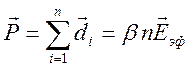 , (6.11)
, (6.11)
где
![]() - концентрация неполярных молекул. В
слабых полях (в линейном приближении) имеет место линейная связь между
- концентрация неполярных молекул. В
слабых полях (в линейном приближении) имеет место линейная связь между ![]() ,
, ![]() и
вектором поляризации
и
вектором поляризации ![]() . В общем случае такую связь можно
представить в виде
. В общем случае такую связь можно
представить в виде
![]()
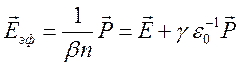 , (6.12)
, (6.12)
где
![]() . Второе равенство в(6,12) дает связь между
. Второе равенство в(6,12) дает связь между
![]() и
и ![]()
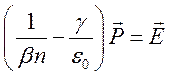 ,
, 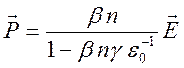 . (6.13)
. (6.13)
Так
как ![]() , то получаем представление для вектора
электрической индукции
, то получаем представление для вектора
электрической индукции
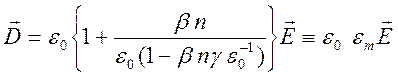 ,
,
где
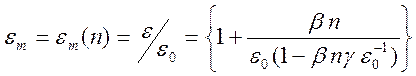 .
.
Эту формулу можно преобразовать, представив в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.