Усилители. Транзистор, как линейный усилитель. Реальные схемы каскадов усиления. Обратные связи в усилителях, страница 9

Рассмотрим подробно эмиттерный повторитель, рис. 6.29а. Сначала мы проиллюстрируем использование общей формулы  для усилителей с обратной связью, полученной на основе равенства . Нам надо найти  и . Для данного примера на средних частотах (ёмкости  и  закорачиваем) . Сравнивая эти равенства, имеем:  (100% обратная связь). Найдём коэффициент усиления без обратной связи . ; , где  есть входное сопротивление каскада без обратной связи (). Тогда , а .                     (6.10) Здесь  - динамическая крутизна транзистора. В результате, усиления по напряжению нет (по току и по мощности есть). Обычно  и . Отсюда название каскада, повторитель напряжения.

Другие параметры: . , если .                         (6.11)  При этом, выходное сопротивление определяется крутизной транзистора (лампы), и для мощных транзисторов может составлять единицы ом. Итак, входное сопротивление большое, выходное – малое. Это и есть главная особенность повторителей. Они очень широко используются как согласующие, «буферные» каскады.

В качестве полезного упражнения, получим те же результаты с эквивалентной схемой, изображённой на рис. 6.30. Рассмотрим средние частоты, поэтому ёмкости не учитываем. Не будем, для простоты, учитывать и , поскольку оно стоит параллельно входу (его легко учесть отдельно). Пишем систему уравнений для токов  и . . . Обычно .

;  .

Из второго уравнения: 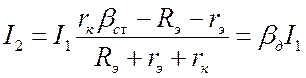, где .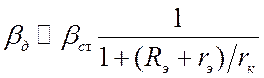
Из первого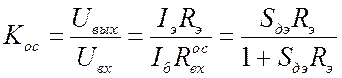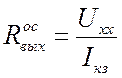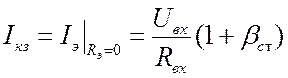: ; . .  . ;  , т. к. при коротком замыкании выхода внешней обратной связи нет. В итоге: . За счёт внешнего сопротивления  реализуется внешняя обратная связь, за счёт  – внутренняя, которая всегда существует.

Формулы для коэффициента передачи и выходного сопротивления истокового и катодного повторителя совершенно аналогичны, только обозначения разные. Напишем для первого. ;  , если . . Сопротивление , рис. 6.29в, определяет необходимое смещение на затворе (по постоянной составляющей). Обычно .

Входное сопротивление определяется иначе. Напишем закон Ома для участка цепи, содержащего  (для средних частот, без учёта ёмкостей). . 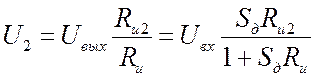; 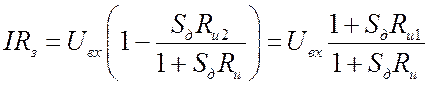. Входное сопротивление . Оно может быть огромным ( и больше).

6.4.4. Другие примеры усилителей с обратной связью.

1. Однокаскадный усилитель. Самый простой вариант ООС получается при наличии сопротивления  в цепи эмиттера, рис. 6.11. Мы это уже обсуждали. Коэффициент усиления уменьшается за счёт увеличения . Без обратной связи (): . При наличии обратной связи: ;  . Последнее выражение легко преобразовать к виду, характерному для усилителей с ОС. 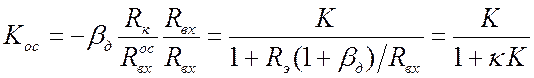, где 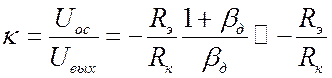 есть коэффициент передачи цепи обратной связи.

Этот результат мы можем получить иначе, более прямым путём. Напряжение , непосредственно управляющее током транзистора, есть разность двух синфазных напряжений, , где . Отсюда, учитывая равенства  и , получим . Эта формула отличается от приведённой ранее формулы 6.9 знаком в знаменателе, за счёт изменения знака у величины . Здесь так удобнее.

Таким образом, наличие сопротивления  приводит к уменьшению напряжения  по сравнению со входным и, как результат, к уменьшению усиления. Это и есть типичная отрицательная обратная связь.

Как организовать положительную обратную связь в однокаскадном усилителе? Сигнал на выходе усилителя противофазен по отношению к входному. Поэтому цепь обратной связи должна дать дополнительный фазовый сдвиг на . Это можно сделать, например, с помощью трансформатора.

2. Двухкаскадный усилитель. Теперь напряжения входное и выходное оказываются синфазными. Подавая часть выходного напряжения на вход, например так, как указано на рис. 6.31 (без сдвига фаз), мы получим положительную ОС. Такой вариант ОС широко используется в различных генераторах.