Усилители. Транзистор, как линейный усилитель. Реальные схемы каскадов усиления. Обратные связи в усилителях, страница 17

Получите самостоятельно выражение для коэффициента усиления реального ОУ, с учётом . .

Отметим одну  интересную особенность схемы инвертирующего усилителя. С одной стороны, мы говорим о большом входном сопротивлении ОУ  . С другой стороны, , а следовательно, сопротивление между инвертирующим входом и общим проводом (землёй) стало очень маленьким (). Однако никакого парадокса тут нет. Это типичное влияние глубокой параллельной ООС. Она обеспечивает малое сопротивление. Если ОС нет (), то и сопротивление будет большим.

Когда мы хотим сделать полосовой усилитель (постоянная составляющая  нам не нужна), то последовательно с сопротивлением  мы ставим конденсатор, как на рис. 6.46б. Теперь на входе образовалась дифференцирующая цепь с постоянной времени . . Тогда , а . Нижняя граничная частота полосы пропускания усилителя на уровне 0,71 будет .

Вопрос о верхней граничной частоте мы обсудим в следующем параграфе.

6.8.2. Неинвертирующий усилитель.

Схема усилителя и обозначения приведены на рис. 6.47а. ; ;   есть коэффициент передачи цепи ОС. . . Пишем очевидное равенство. . Деля его на , получим .        (6.13) Для идеального ОУ () . В результате .                                                                                            (6.14)

Входное сопротивление для такой схемы огромно, поскольку большое собственное входное сопротивление ОУ, увеличено ещё за счёт глубокой последовательной ООС.

Обсудим теперь важный вопрос о верхней граничной частоте полосы пропускания. Она определяется, как правило, цепью частотной коррекции или нагрузкой. В любом случае мы можем считать, что частотная зависимость коэффициента усиления ОУ без внешней ООС на высоких частотах такая же, как для одной интегрирующей цепочки с постоянной времени . Если усилитель линеен, то неважно где цепочка находится; важно, что она есть.

Итак . Теперь учтём ООС и воспользуемся формулой (6.13), подставив туда  вместо . Мы это уже делали, когда обсуждали ОС. Сделаем это ещё раз. ,            (6.15)
где . Таким образом, эффективная постоянная времени  и верхняя граничная частота  зависят от глубины ООС. Чем сильнее ООС, тем меньше  и тем шире полоса. Между этими величинами получается обратно пропорциональная зависимость. Для данного ОУ произведение  постоянно. Параметр  часто приводится в справочниках для ОУ и имеет смысл граничной частоты при единичном усилении (повторитель). Зная указанную зависимость и , легко оценить верхнюю граничную частоту по заданному усилению. Отмеченная закономерность справедлива и для инвертирующего усилителя.

Если мы хотим получить полосовой усилитель, то опять ставим конденсатор последовательно с генератором и сопротивление , как на рис. 6.47б. На входе образовалась дифференцирующая цепь с постоянной времени . Нижняя граничная частота . . Сопротивление  в этом случае определяет входное сопротивление усилителя. Но у него есть и другая роль. Если его не поставить, а конденсатор окажется «достаточно» идеальным, то постоянная составляющая тока неинвертирующего входа не сможет нормально протекать во входной цепи. Какая бы она не была маленькая, она всё равно есть. Надо обязательно организовать для неё цепь. Поэтому такие сопротивления часто называют сопротивлениями «утечки».

6.8.3. Повторитель напряжения.

Это неинвертирующий усилитель с коэффициентом усиления равным единице, рис. 6.47в. Такой коэффициент усиления получится, если . Тогда  можно не ставить (). Реализуется очень сильная ООС (). Входное сопротивление огромно, выходное - самое маленькое, полоса пропускания самая широкая для данного ОУ.

6.8.4. Интегрирующий усилитель.

Он представляет собой инвертирующий усилитель, в котором , а , рис. 6.48. Тогда коэффициент передачи такого усилителя даёт оператор интегрирования. , где . Пусть , когда . При , будем иметь 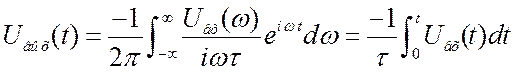. Получился качественный аналоговый интегратор, но не идеальный, поскольку мы не учли реальные параметры ОУ. Так можно реализовать постоянные времени  десятки, даже сотни секунд, сохраняя малое выходное сопротивление за счёт ОУ.