Усилители. Транзистор, как линейный усилитель. Реальные схемы каскадов усиления. Обратные связи в усилителях, страница 3

В результате, получим эквивалентную схему, изображённую на рис. 6.9.  для второй схемы и просто для первой. Цепь с  не показана. Её влияние мы обсудим позже отдельно. Схема представляет типичный полосовой фильтр. Качественная зависимость  такого фильтра изображена на рис. 6.21.  максимален на частоте , . Спад характеристики в области нижних частот определяется двумя дифференцирующими цепочками (ёмкости  и ). Спад в области верхних частот даёт выходная интегрирующая цепочка с ёмкостью . Интегрирующая цепочка пока одна, но мы скоро убедимся, что их будет несколько.

Широкополосность каскада означает, что граничные частоты полосы пропускания каскада удовлетворяют сильному неравенству  (по крайней мере, на один, два порядка). Это обстоятельство позволяет упростить задачу и анализировать зависимость  отдельно на низких (), средних () и высоких частотах (). В каждом из этих диапазонов мы упрощаем схему, оставляя только существенные элементы. Так, на низких частотах мы можем не учитывать ёмкость интегрирующей цепочки (положить ), а на высоких – ёмкости  и  (закоротив их). Если мы при этом и ошибёмся немного количественно, то это не страшно. В учебном курсе нам прежде всего важны качественные закономерности.

6.3.2. Анализ ШУ на средних частотах.

В этом диапазоне коэффициент усиления каскада  меняется очень мало и мы можем не учитывать влияние всех конденсаторов и инерцию транзистора. Фактически мы определяем . На эквивалентной схеме останутся одни сопротивления и зависимый генератор, рис. 6.10. Сопротивление  опущено, поскольку оно шунтировало входной генератор с малым сопротивлением, а два параллельных сопротивления на выходе заменены одним, .

Пишем систему уравнений Кирхгофа для двух токов.  ; . Из второго уравнения выражаем ток коллектора 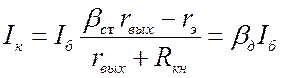и вводим  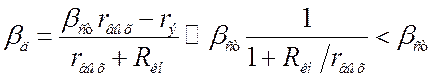         (6.3) Это уже динамический параметр, который зависит от внешних сопротивлений. В последнем выражении учтено сильное неравенство (). Первое уравнение, после исключения тока  даёт: . Отсюда мы определяем входное сопротивление транзистора с учётом нагрузки  (она вошла в ). .                                                                        (6.4)

Выходное напряжение . Тогда коэффициент усиления каскада на средних частотах .  (6.5) Здесь 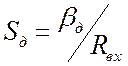 есть динамическая крутизна, важный усилительный параметр транзистора. Отметим знак минус. Он означает изменение фазы выходного напряжения на , по отношению к входному, и отражает тот факт, что с ростом ,  уменьшается. Минус получится для любого транзистора и лампы.

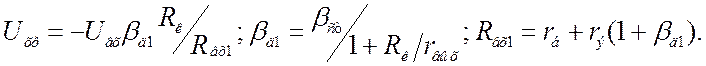
Выходное сопротивление каскада (без учёта ) определяется отношением напряжения холостого режима () к току короткого замыкания (, статический режим).  . В итоге: 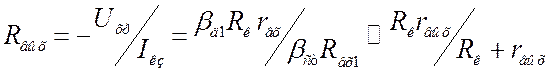.   (6.6) Если  (тогда и ), то  Этот результат очевиден из эквивалентной схемы каскада, где  стоит параллельно выходу и минимально.

6.3.3. Влияние сопротивления в цепи эмиттера.

Часто в цепь эмиттера ставят внешнее сопротивление , рис. 6.11. Оно оказывается включённым последовательно с  на эквивалентной схеме (они совершенно равноправны). Следовательно, если мы хотим учесть , то в формулу для  надо вместо  подставить сумму . . Изменяется и выходное сопротивление, но незначительно. Наличие сопротивления в цепи эмиттера увеличивает входное сопротивление каскада, но уменьшает усиление. Это самый простой и эффективный способ увеличения .

Отметим интересное обстоятельство. Если  и , то  и  уже не зависит от параметров транзистора.

6.3.4. Каскад усиления на лампах и полевых транзисторах.

Рассмотрим работу только транзисторного каскада на средних частотах, рис. 6.12. Для лампового каскада всё аналогично, только обозначения другие. Поясним назначение новых элементов.  есть сопротивление «утечки» затвора. Постоянная составляющая тока затвора реально существует; какая бы маленькая она ни была, но она есть. Надо дать возможность зарядам стекать на общий провод. Падения напряжения на этом сопротивлении, практически, нет, поэтому потенциал затвора равен нулю.