Усилители. Транзистор, как линейный усилитель. Реальные схемы каскадов усиления. Обратные связи в усилителях, страница 18

6.8.5. Аналоговый сумматор.

Это есть инвертирующий усилитель, на вход которого поданы два (или больше) напряжения параллельно, рис. 6.49. Проведём рассуждения, считая ОУ идеальным. . В результате . Выходное напряжение оказывается пропорциональным сумме входных токов. Если взять одинаковые сопротивления , то  . Получается достаточно качественный сумматор.

Напряжения  оказываются «развязанными», не влияющими друг на друга, поскольку  и сопротивление между этими узлами схемы тоже мало (). Так можно суммировать значительное число напряжений (порядка десятка). Эта схема находит широкое применение, например, в цифроаналоговых преобразователях (ЦАП).

6.8.6. Активные фильтры.

Схема активного фильтра изображена на рис. 6.50а. При анализе схемы мы можем считать, что ОУ работает в режиме неинвертирующего усилителя с заданным коэффициентом усиления . Однако здесь имеется ещё одна ОС, которую надо учесть. Для этого перейдём к эквивалентной схеме, рис. 6.50б, заменив ОУ эквивалентным разорванным  четырёхполюсником с параметрами:  (параграф 6.2.2, рис. 6.5б). Фактически, остаётся один идеальный генератор с ЭДС . Цепь ООС уже учтена, путём введения .

Пишем систему уравнений Кирхгофа для двух связанных контуров. ;  . Определитель системы . Для определения коэффициента передачи фильтра , нас интересует только ток , поскольку . . Теперь пишем следующее равенство. . Делим последнее равенство на  и получаем результат: .               (6.16)
Для пассивного фильтра (рис.6.50в) мы имели . В активном фильтре введена дополнительная ОС, которая позволяет улучшить качество фильтра по сравнению с пассивным. Рассмотрим это подробнее на примере ФНЧ.

6.8.6.1. Активный фильтр НЧ.

Его схема приведена на рис. 6.51. В данном случае: ; . , где .                               (6.17)
Если , т.е. ОУ работает в режиме повторителя, то: ; ; .

С помощью активного фильтра можно реализовать любые значения параметра , даже отрицательные, которым соответствует неустойчивый режим. Напомним, что качество фильтра улучшается с уменьшением , но предельное значение  для ФНЧ равно 0,76. Приведём четыре примера выбора параметров фильтра.

1. . Тогда . Коэффициент прямоугольности . Для пассивного фильтра при этом   ().

2. 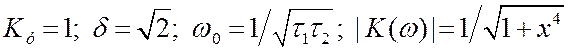. Получается фильтр Баттерворса, . Если , то . Пассивный RC фильтр с таким значением  реализовать невозможно.

3. . Как для пассивного LC фильтра с добротностью единица. Максимум  реализуется уже не на нулевой частоте («выброс» примерно 17%) , . Если , то .

4. . Реализуется неустойчивость, возбуждение.

Обычно отмечают два основных преимущества активных фильтров по сравнению с пассивными.

1. Малое выходное сопротивление активного фильтра, определяемое ОУ. При этом не надо согласовывать элементы фильтра с параметрами нагрузки. ОУ играет роль «буферного» устройства.

2. С помощью активного фильтра можно получить частотные характеристики, как у пассивных LC фильтров, но без индуктивностей.

6.8.6.2. Активный фильтр ВЧ.

Теперь сопротивления и конденсаторы поменялись местами, рис. 6.52. Приведём здесь только некоторые формулы без вывода и комментариев. Все неотмеченные обозначения параметров сохраняются. , где теперь . Когда , ; . Если , то .

6.8.6.3. Активный полосовой фильтр.

Один из вариантов реализации активного полосового фильтра изображён на рис. 6.53а. Он представляет собой инвертирующий усилитель с обратной связью. Эквивалентная схема такого усилителя изображена на рис. 6.53б. Для упрощения рассуждений будем считать ОУ идеальным. Пишем систему уравнений. ;  . Определитель системы . Нас опять интересует только ток , поскольку . Подставляя сюда ток , будем иметь равенство: . Отсюда .                                                                   (6.18) Это выражение можно записать иначе: , где  есть коэффициент передачи пассивного полосового фильтра второго порядка, который получается комбинацией дифференцирующей и интегрирующей цепочек (параграф 3.8.5.3, глава 3).