Аналогично вводят
параметры ![]() и
и ![]() для
схемы с общей базой (
для
схемы с общей базой (![]() ). Пишут
). Пишут ![]() .
Найдём связь между введёнными параметрами. Поскольку
.
Найдём связь между введёнными параметрами. Поскольку ![]() ,
то
,
то ![]() . Отсюда
. Отсюда ![]() . В
справочниках по транзисторам приводятся частоты
. В
справочниках по транзисторам приводятся частоты ![]() и
и ![]() . Это частоты, на которых коэффициенты
передачи тока
. Это частоты, на которых коэффициенты
передачи тока ![]() и
и ![]() уменьшаются
в
уменьшаются
в ![]() раз за счёт инерции транзистора. Иногда
приводится частота
раз за счёт инерции транзистора. Иногда
приводится частота ![]() , на которой
, на которой ![]() (частота единичного усиления). Это
равенство реализуется, когда
(частота единичного усиления). Это
равенство реализуется, когда ![]() (
(![]() ), поэтому
), поэтому ![]() .
Различают транзисторы низкочастотные (
.
Различают транзисторы низкочастотные (![]() гц),
высокочастотные (
гц),
высокочастотные (![]() ) и СВЧ (
) и СВЧ (![]() и
больше).
и
больше).
6.3.7. Анализ каскада ШУ на высоких частотах.
Изобразим опять схему каскада,
добавив три новых конденсатора ![]() и
и ![]() , рис. 6.17. В них включены все возможные
ёмкости, монтажа, переходов и пр. Вот и появились новые интегрирующие цепочки.
Постараемся упростить схему. В этом диапазоне частот мы можем не учитывать
конденсаторы
, рис. 6.17. В них включены все возможные
ёмкости, монтажа, переходов и пр. Вот и появились новые интегрирующие цепочки.
Постараемся упростить схему. В этом диапазоне частот мы можем не учитывать
конденсаторы ![]() и
и ![]() дифференцирующих
цепочек. Не будем также учитывать
дифференцирующих
цепочек. Не будем также учитывать ![]() и
и ![]() , поскольку они включены параллельно входу.
Эти элементы всегда можно учесть отдельно вместе с сопротивлением генератора.
Их роль ясна.
, поскольку они включены параллельно входу.
Эти элементы всегда можно учесть отдельно вместе с сопротивлением генератора.
Их роль ясна.
Рисуем эквивалентную
схему, рис. 6.18. Здесь мы добавили ещё ёмкость ![]() входного
перехода и ввели
входного
перехода и ввели ![]() , как суммарную ёмкость параллельную
нагрузке. Введём обозначения:
, как суммарную ёмкость параллельную
нагрузке. Введём обозначения: ![]() ;
;![]() ;
; ![]() ;
; ![]() . Теперь мы учитываем и инерцию
транзистора, считая
. Теперь мы учитываем и инерцию
транзистора, считая ![]() . Имеем три независимых контура.
Вводим три тока, указанных на рисунке, и пишем систему уравнений.
. Имеем три независимых контура.
Вводим три тока, указанных на рисунке, и пишем систему уравнений. ![]() ;
;
![]() ;
;
![]() .
.
Из последнего уравнения
выражаем ![]() и подставляем во второе. Получаем связь
входного и выходного токов.
и подставляем во второе. Получаем связь
входного и выходного токов. ![]() .
.
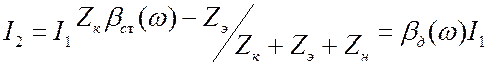 ,
где
,
где 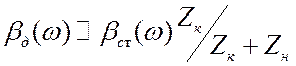 , т.к.
, т.к. ![]() . Из
первого уравнения
. Из
первого уравнения ![]() . Отсюда
. Отсюда ![]() .
Поскольку
.
Поскольку ![]() , то коэффициент усиления
, то коэффициент усиления ![]() . Наконец, прямо из эквивалентной схемы,
можно приближённо выразить
. Наконец, прямо из эквивалентной схемы,
можно приближённо выразить ![]() (здесь
(здесь ![]() ).
).
В итоге мы получили
формулы, как для средних частот, только ![]() и все
сопротивления (кроме
и все
сопротивления (кроме ![]() ) теперь стали комплексные, стали
функциями частоты. Модули всех этих комплексных величин уменьшаются с ростом
частоты, стремясь к нулю, но каждая зависит от своего параметра. Имеем 4 постоянные
времени:
) теперь стали комплексные, стали
функциями частоты. Модули всех этих комплексных величин уменьшаются с ростом
частоты, стремясь к нулю, но каждая зависит от своего параметра. Имеем 4 постоянные
времени: ![]() и
и ![]() . Всё
определяет их соотношение. Надо постараться выделить главные, наибольшие.
. Всё
определяет их соотношение. Надо постараться выделить главные, наибольшие.
Приведём некоторые
оценки: ![]() ф,
ф, ![]() ом,
ом, ![]() сек.;
сек.; ![]() ф,
ф, ![]() ком,
ком, ![]() сек.;
сек.; ![]() ф,
ф, ![]() ком,
ком, ![]() сек.
сек. ![]() зависит
от типа транзистора и меняется в широких пределах. Обычно
зависит
от типа транзистора и меняется в широких пределах. Обычно ![]() и
и ![]() самые
маленькие, если транзистор выбран правильно. Остаются два главных параметра,
самые
маленькие, если транзистор выбран правильно. Остаются два главных параметра, ![]() и
и ![]() .
Выясним прежде всего их влияние порознь.
.
Выясним прежде всего их влияние порознь.
1. Влияние ёмкости
нагрузки ![]() . В учебниках чаще всего рассматривают
именно эту типичную ситуацию, когда наибольшей является
. В учебниках чаще всего рассматривают
именно эту типичную ситуацию, когда наибольшей является ![]() .
Она определяет верхнюю граничную частоту и общую полосу пропускания. Итак,
учитываем только ёмкость
.
Она определяет верхнюю граничную частоту и общую полосу пропускания. Итак,
учитываем только ёмкость ![]() и считаем
и считаем ![]() . Все остальные величины
. Все остальные величины ![]() - вещественны (
- вещественны (![]() ).
Имеем одну интегрирующую цепочку на выходе каскада. Подставляя нужные величины
в формулы, будем иметь:
).
Имеем одну интегрирующую цепочку на выходе каскада. Подставляя нужные величины
в формулы, будем иметь: ![]()
![]() ;
; ![]() ;
; ![]() , если
, если ![]() .
.
Теперь  при
при ![]() .
Частота
.
Частота ![]() есть верхняя граничная частота полосы
пропускания на уровне 0,71. Если неравномерность характеристики на высоких
частотах
есть верхняя граничная частота полосы
пропускания на уровне 0,71. Если неравномерность характеристики на высоких
частотах ![]() имеет другое значение, то
имеет другое значение, то 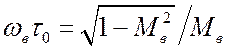 .Хотя слабая зависимость
.Хотя слабая зависимость ![]() от частоты существует (
от частоты существует (![]() при
при ![]() ), но в
полосе пропускания (
), но в
полосе пропускания (![]() ) она практически не проявляется
и её можно не учитывать. Выходное сопротивление уменьшается с ростом частоты.
) она практически не проявляется
и её можно не учитывать. Выходное сопротивление уменьшается с ростом частоты.
2. Влияние ёмкости ![]() . Пусть
. Пусть![]() .
. ![]() . Все остальные величины (
. Все остальные величины (![]() ) - вещественны. Имеем одну интегрирующую
цепочку. Вычисления дают:
) - вещественны. Имеем одну интегрирующую
цепочку. Вычисления дают: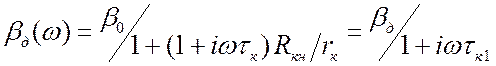 , где
, где 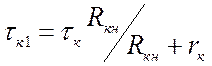 .
. ![]() .
. 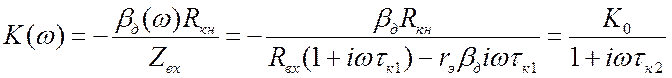 , где
, где 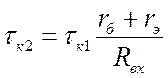 .
. 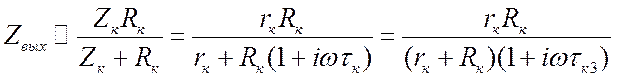 ;
; 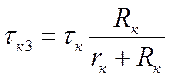 .
.
Все вычисленные величины
стали комплексны и их модули убывают с ростом частоты, но эффективные
постоянные времени, описывающие это убывание (![]() ),
оказываются много меньше
),
оказываются много меньше ![]() . Сама постоянная
. Сама постоянная ![]() в формулы не входит. В результате, влияние
интегрирующей цепочки с ёмкостью
в формулы не входит. В результате, влияние
интегрирующей цепочки с ёмкостью ![]() значительно ослаблено.
Проиллюстрируем это на простом примере. Пусть
значительно ослаблено.
Проиллюстрируем это на простом примере. Пусть ![]() . Тогда:
. Тогда:
![]() . Влияние
. Влияние ![]() никак
не проявилось, как будто её нет. Входное сопротивление уменьшается с ростом
частоты, стремясь к значению
никак
не проявилось, как будто её нет. Входное сопротивление уменьшается с ростом
частоты, стремясь к значению ![]() . Структура формулы
позволяет нарисовать эквивалентную схему входной цепи, изображённую на рис.
6.19. Во входной цепи появилась ёмкость
. Структура формулы
позволяет нарисовать эквивалентную схему входной цепи, изображённую на рис.
6.19. Во входной цепи появилась ёмкость ![]() за
счёт
за
счёт ![]() .
.
3. Рассмотрим отдельно
влияние инерции транзистора. Никаких конденсаторов теперь нет, все
сопротивления вещественны. Вычислим параметры каскада. ![]() ;
;
![]() .
. ![]() .
. ![]() .
. 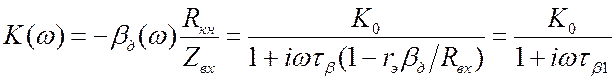 , где
, где 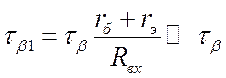 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.