Усилители. Транзистор, как линейный усилитель. Реальные схемы каскадов усиления. Обратные связи в усилителях, страница 4

Сопротивление  в цепи истока образует цепь автоматического смещения. Для нормальной работы транзистора с n – каналом на затвор надо подать постоянное отрицательное напряжение смещения по отношению к истоку, или на исток – положительное по отношению к затвору. Последнее и достигается за счёт падения напряжения на сопротивлении . В итоге, исток имеет необходимый положительный потенциал, а затвор – нулевой. Однако наличие сопротивления в цепи истока, если оно не зашунтировано конденсатором большой ёмкости, приведёт к образованию отрицательной обратной связи по переменной составляющей и значительному уменьшению коэффициента усиления каскада (как ). Когда это не желательно, параллельно сопротивлению ставят конденсатор . К этому мы ещё вернёмся.

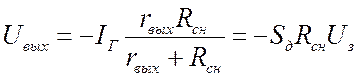Для анализа работы каскада транзистор удобно заменить эквивалентным разорванным четырёхполюсником, рис. 6.13. Собственное входное сопротивление транзистора очень большое (), а обратная связь, практически, отсутствует (). Поэтому входная цепь упрощается. На средних частотах конденсаторы  и  закорачиваем. Тогда: ; ; . , где 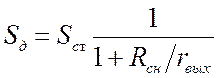. . Эта формула универсальна. , если .

6.3.5. Анализ каскада ШУ на низких частотах.

Вернёмся к усилителю на биполярном транзисторе и рассмотрим входную и выходную цепи отдельно. В этом диапазоне считаем  и инерцию транзистора не учитываем. Входная цепь изображена на рис. 6.14. Учёт ЭДС обратной связи E₁ вместе с  даёт .  есть напряжение непосредственно на входе транзистора. . Обычно . Входное сопротивление каскада теперь комплексно, . Коэффициент передачи для входной цепи , где , тоже комплексный, как для дифференцирующей цепочки.

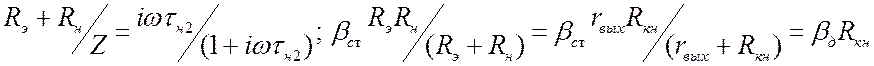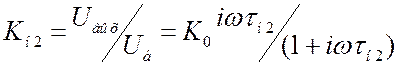Выходная цепь изображена на рис. 6.15. Здесь мы воспользовались теоремой об эквивалентном генераторе для упрощения цепи. ; ; . . Теперь учтём два равенства: . Коэффициент усиления для выходной цепи , где  есть коэффициент усиления на средних частотах.

Общий коэффициент усиления каскада на низких частотах мы получим, перемножив коэффициенты для входной и выходной цепей, поскольку  мы определили с учётом выходной цепи. 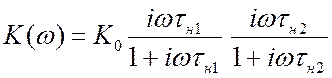.              (6.7)

Проявили себя обе дифференцирующие цепочки. Для одной цепочки неравномерность характеристики 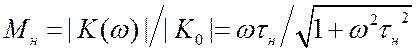. Пусть определённая неравномерность  задана на частоте , тогда 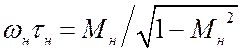. Если , то . Для двух цепочек, общую неравномерность  можно распределить на две цепочки  и расчёт производить для каждой отдельно.

Выходное сопротивление каскада тоже становится комплексным на низких частотах. .

6.3.6. Учёт инерционных свойств транзистора.

На высоких частотах начинает проявлять себя инерция процессов в самом транзисторе. В основном, это время диффузии или дрейфа носителей в базе (время пролёта электронов в лампе) и другие процессы. Кроме этого, параллельно каждому p – n переходу мы должны включить конденсаторы. Они будут заряжаться и разряжаться. Тоже инерция.

Ёмкости учесть проще. Мы изобразим на эквивалентной схеме нужное число конденсаторов и учтём их при анализе схемы. Как можно учесть инерцию самого транзистора? Аккуратно это сделать совсем не просто. Надо изучать кинетику носителей, оценивать времена диффузии и дрейфа. Простейший подход основан не на детальном анализе процессов, а на моделировании проявлений. Рассуждают так. Инерция есть. Как она проявляется? Если изменить ток базы скачком, то ток в коллекторной цепи будет меняться непрерывно, как на рис. 6.16. Процесс установления тока коллектора описывается сложной функцией с несколькими параметрами. Однако, в самом грубом приближении, мы можем апроксимировать весь этот процесс простой экспоненциальной функцией с некоторой постоянной времени . . Такой процесс даёт простая интегрирующая цепочка. Мы получим этот процесс в качестве переходной характеристики транзистора, если предположим, что усилительный параметр  транзистора зависит от частоты, как коэффициент передачи интегрирующей цепочки. .                                                                      (6.8) Такой простой функцией частоты с одним параметром  моделируются в грубом приближении инерционные свойства транзистора на высоких частотах. Задают обычно не , а частоту  ().