Трехфазные цепи. Многофазные цепи. Симметричные и несимметричные режимы трёхфазных цепей. Метод симметричных составляющих, страница 5

Средняя активная мощность в каждой фазе , где  и   - амплитуды фазных напряжений и токов. Удобно эту мощность выразить через линейные напряжения и токи. Если нагрузки соединены звездой, то , а . Если же нагрузки соединены треугольником, то , а . Поэтому независимо от варианта соединения нагрузок,  среднюю фазную мощность можно выразить через линейные величины  . Тогда суммарная активная мощность трёх фаз .                                                                                     (6.4) Здесь  есть сдвиг фаз между напряжением и током в каждой фазе нагрузки.

Аналогичные равенства можно написать и для амплитуды реактивной мощности. Так, амплитуда суммарной реактивной мощности трёх фаз .                                                                                       (6.5)

6.3. Несимметричные режимы трёхфазных цепей.

Будем для простоты считать генераторы идеальными и не учитывать падение напряжения в них, а нагрузку – статической, без движущихся частей. Различные двигатели мы рассмотрим позже. Тогда расчёт несимметричных режимов трёхфазных цепей не содержит ничего нового по сравнению с однофазными. По-прежнему общая тенденция выражается в том, чтобы упростить цепь и перейти к однофазным цепям, несвязанным. Рассмотрим ряд примеров, отражающих типичные ситуации.

6.3.1.  Пересчёт сопротивлений, включённых звездой и треугольником.

Две интересующие нас схемы приведены на рис. 6.12. Мы хотим написать условия их эквивалентности, позволяющие одну схему заменить другой. Необходимость такой операции возникает очень часто при анализе реальных цепей. Напишем условия равенства сопротивлений между соответствующими узлами этих схем:           , где . Из этой системы легко получить  результат: .                (6.6)   Обращая эти равенства, будем иметь:

.   (6.7) Если, например, , то .

6.3.2. Цепь с нулевым проводом.

Ситуация изображена на рис. 6.13. Она типична для оконечного звена энергетических линий, где нулевой провод (нейтраль) всегда есть. Вторичные обмотки понижающего трансформатора соединяются звездой и общий вывод заземляется. Наличие нейтрали позволяет включать нагрузки на линейное напряжение (380 вольт) и на фазное (220), треугольником и звездой. Сопротивление проводов линии учтены в нагрузках.

Задана несимметричная система фазных напряжений генераторов ,  и нагрузки, соединённые звездой. Требуется определить токи в нагрузках и нейтрали. В этой ситуации соединение нагрузок звездой удобнее для анализа, поскольку оно позволяет быстрее и проще перейти к однофазным цепям. Формулы упрощаются, если вместо сопротивлений нагрузок ввести проводимости .

Следует отметить, что в данном случае три фазных напряжения являются независимыми. Они позволяют однозначно определить и линейные напряжения.

Схема имеет два узла и четыре ветви. Воспользуемся методом узловых потенциалов. Пусть  есть искомое напряжение между узлами. Тогда  токи ветвей таковы: ; .
Сумма этих токов даёт ток нейтрали . Подставляя в это равенство токи ветвей, будем иметь: , где . Отсюда 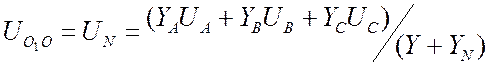 .         (6.8) Теперь мы можем найти все токи и фазные напряжения на нагрузках.

Если пренебречь сопротивлением нейтрали, то  и . Тогда ток в каждой фазе находится совершенно независимо.

Нагрузки в этом примере могут быть соединены произвольным образом, однако во многих случаях их можно привести к рассмотренному варианту путём эквивалентных преобразований.

В том случае, когда по каким-то причинам возникают проблемы при определении напряжения между узлами, можно использовать метод последовательных приближений. Реальный (штатный) режим работы трёхфазной цепи обычно близок к симметричному. Тогда ток в нейтрали значительно меньше, чем ток в линейных проводах. Следовательно и падение напряжения  мало по сравнению с фазным (5-10%). В первом приближении мы можем его не учитывать и считать . Найдя приближённо токи в фазах нагрузки и ток в нейтрали, мы сможем оценить величину  и, при необходимости, уточнить результат.

Приближённые методы находят очень широкое применение, в том числе и векторные диаграммы. Точные расчёты часто бессмысленны, поскольку ситуация всё время меняется. Приближённый расчёт полезен ещё и потому, что он позволяет проще оценить результат.