Трехфазные цепи. Многофазные цепи. Симметричные и несимметричные режимы трёхфазных цепей. Метод симметричных составляющих, страница 11

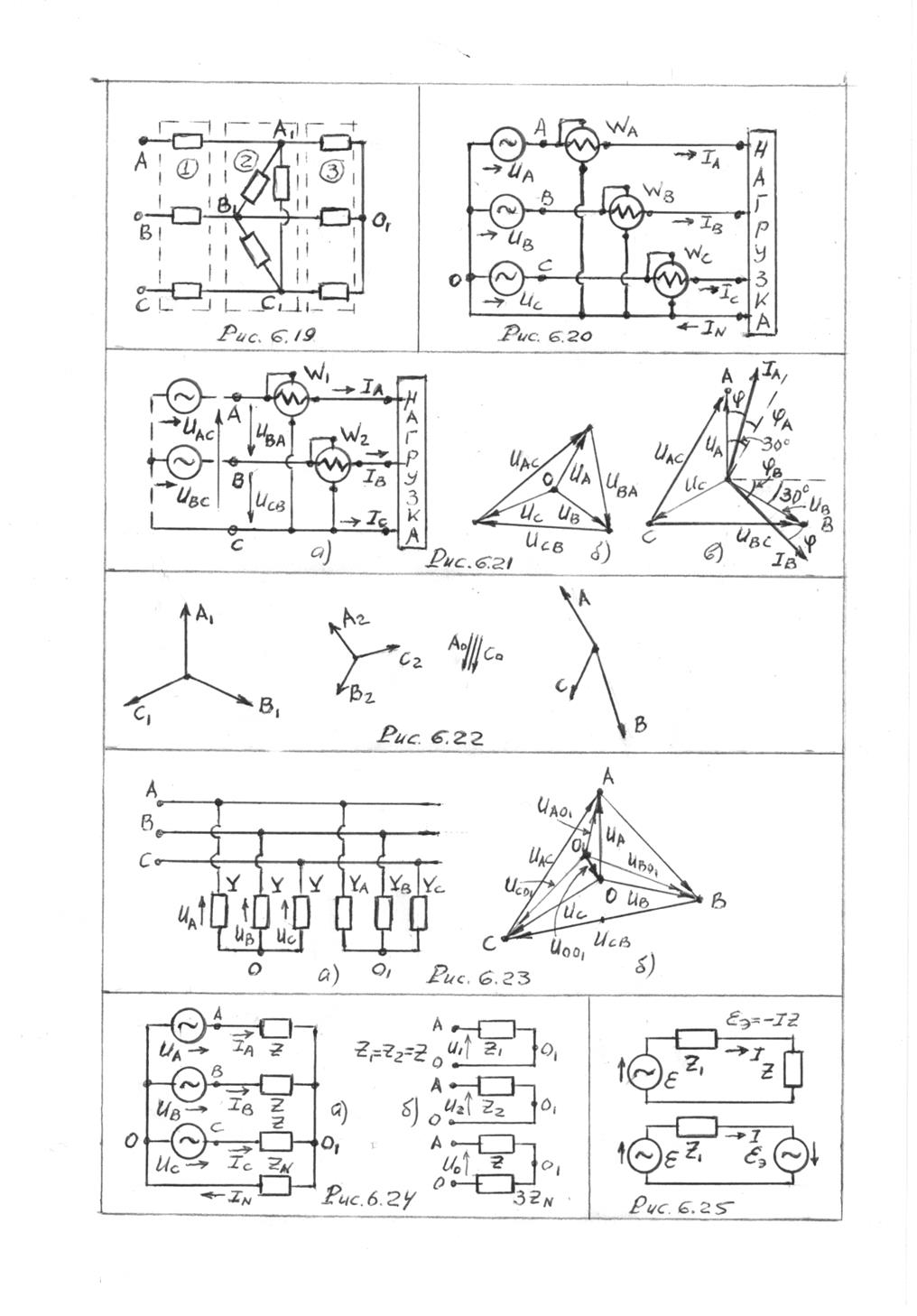
Рассмотрим снова цепь предыдущего пункта, изображённую на рис. 6.24а, только теперь все нагрузки могут быть разные. Ситуация стала значительно сложнее. Если на такую цепь подать симметричную систему напряжений любой последовательности, то в ней возникнет несимметричная система токов, которая, в общем случае, содержит составляющие всех трёх последовательностей. Справедливо и обратное утверждение. Симметричная система фазных токов любой последовательности породит в такой цепи несимметричную систему фазных напряжений, которая может содержать составляющие всех трёх последовательностей.

Таким образом, в цепи с несимметричными нагрузками симметричные составляющие токов любой последовательности зависят от симметричных составляющих напряжений всех трёх последовательностей. Проблема возникла из-за несимметрии нагрузок (). Можно несимметричную нагрузку превратить в симметричную или совсем от неё избавиться? Да, можно. В теории цепей есть теорема о замещении (компенсации), которая позволяет любое сопротивление  в цепи с током  заменить идеальным генератором напряжения с ЭДС . Доказать её можно с помощью простых вычислений, показав равенство токов для двух вариантов схемы на рис. 6.25.

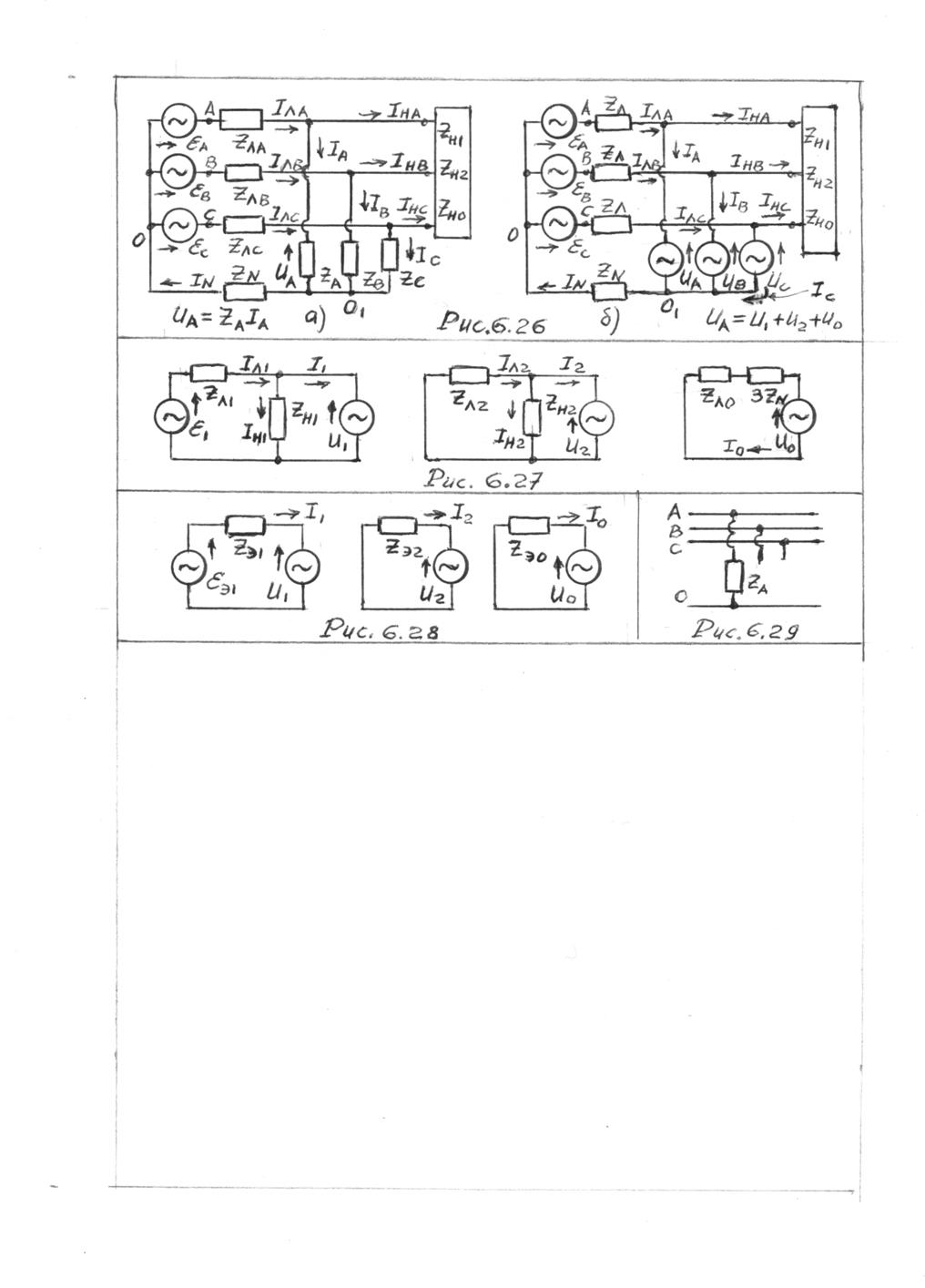
Проиллюстрируем очень коротко идею метода расчёта на примере цепи с нейтралью, изображённой на рис. 6.26а.  Общую нагрузку цепи, включённую звездой,  обычно можно разделить на симметричную и несимметричную части, как указано на рисунке. С симметричной частью нагрузки проблем нет. Она характеризуется тремя сопротивлениями  для симметричных составляющих прямой, обратной и нулевой последовательностей. Несимметричная часть нагрузки задана своими сопротивлениями  (сопротивления разные).  Кроме этого, в этом примере приходится учитывать симметричную систему сопротивлений генератора и линии. На схеме эти сопротивления обозначены как сопротивления линии (). Будем считать для определённости, что нам задана симметричная система фазных ЭДС генератора прямой последовательности  . Требуется найти токи и напряжения на всех участках цепи. Необходимые обозначения указаны на рисунке.

Теперь воспользуемся теоремой о замещении и заменим сопротивления в несимметричной нагрузке тремя идеальными источниками с напряжениями . Тогда мы получим схему с симметричными нагрузками, изображённую на рис. 6.26б, в которой имеются источники с заданной симметричной системой ЭДС (на входе) и источники с несимметричными напряжениями, пока неопределёнными, поскольку мы не знаем токов. Разложим несимметричную систему напряжений  на симметричные составляющие , приняв фазу A за основную.

     .       (6.16)

Для каждой симметричной составляющей теперь мы можем изобразить свою схему, рис. 6.27. Схемы достаточно простые. Режим фазы  A исходной цепи получится наложением режимов этих трёх схем. Схемы прямой и обратной последовательности имеют одинаковую конфигурацию. Схема нулевой последовательности обычно отличается. В данном случае она не имеет разветвления, так как симметричная нагрузка в исходной цепи включена без нулевого провода.

Схемы для отдельных симметричных составляющих после упрощения приведены на рис. 6.28. Параметры этих схем следующие:  . Для этих схем пишем три уравнения, в которых имеется шесть неизвестных  величин::  . (6.17)

Ещё три уравнения, связывающие эти шесть величин, могут быть составлены на основании заданной схемы и параметров несимметричной нагрузки. Пусть, например, несимметричная нагрузка такова:  произвольно, , рис. 6.29. Тогда дополнительные уравнения выглядят так: . Проведём расчёт при условии  (однофазное замыкание на землю). Переписываем дополнительные уравнения, разлагая их на симметричные составляющие.

 .   (6.18) Из двух последних уравнений получим  . С учётом этого, уравнения (6.17) после их сложения дают равенство . Отсюда находим составляющие токов. Симметричные составляющие напряжений на несимметричной нагрузке определяются уже из основной системы уравнений
(6.17).           .

Теперь по схемам на рис. 6.27 можно найти все необходимые симметричные составляющие токов и напряжений. Суммируя их с учётом фазного множителя по формулам (6.14), мы можем определить действительные несимметричные токи и напряжения в любой ветви цепи.