Поле короткой линейной антенны. Принцип перестановочной двойственности. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией

10.13 Поле короткой линейной антенны. Антенна представляет собой линейный проводник, вдоль которого возбуждается переменный ток с определенным распределением по проводнику. Считается, что антенна достаточно тонкая. Рассмотрим линейную антенну в вакууме с возбуждением в центре (Рис.10.10). Считаем, что в антенне создан гармонический ток, плотность которого имеет только одну составляющую 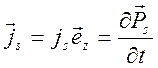 вдоль антенны. Для вектора Герца имеем неоднородное уравнение

                                                .

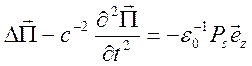Из уравнения видно, что однокомпонентный источник возбуждает только одну компоненту вектора Герца . Решение описывается формулой (10.61):

                                                .

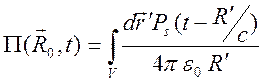Используем факт малости антенны: , ( - расстояние от центра антенны до токи наблюдения ,  - длина волны в вакууме) (Рис.10.11). На основе первого неравенства можно воспользоваться разложением

                                                .

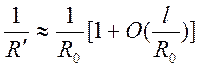Второе неравенство в случае гармонического источника позволяет упростить представление

  ,

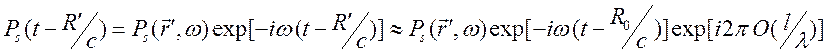где . Использование последнего разложения позволяет пренебречь различием в запаздывании волн от разных точек источника при распространении их в точку наблюдения. В результате приходим к приближенному описанию диполя Герца:

                                                .

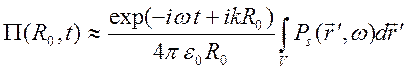Объемный интеграл от плотности дипольного момента источника это полный дипольный момент источника

                                                .

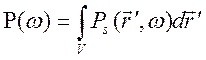Получаем представление

                                                ,

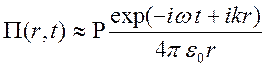где сделана замена . Это описание становится точным для идеализации источника в виде точечного диполя: .

            Обычно задается ток на входе антенны, найдем связь его с дипольным моментом . Учтем, что 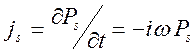 и получим

                        .

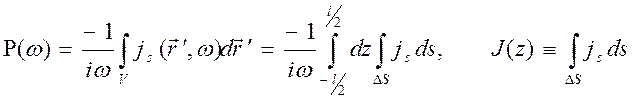 - полный ток в антенне (Рис.10.12). На концах антенны ток равен нулю: . Введем понятие эффективной длинны антенны:

                                                .

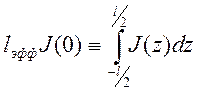При этом имеем представления для дипольного момента и вектора Герца

,                      .

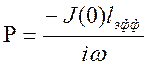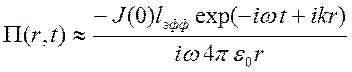На основе последней формулы можно найти поля

                        .

Поле обладает осевой симметрией и в сферической системе координат не зависит от азимутального угла 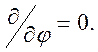 В этой системе координат (Рис.10.13) потенциал  разбивается на две составляющие  Представление  в сферической системе координат имеет вид

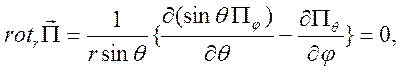
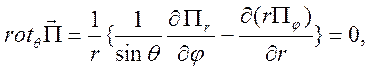
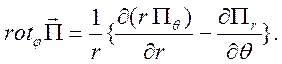
Значит, у магнитного поля есть только азимутальная составляющая

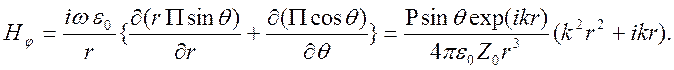
Здесь 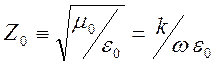 - характеристический импеданс вакуума. Электрическое поле имеет две компоненты

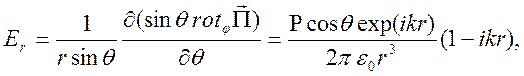
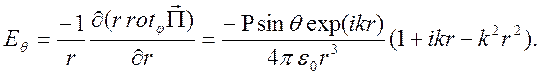
Полученные формулы справедливы для малой линейной антенны, когда выполняются условия . Следовательно, в этих формулах нельзя переходить к пределу

            Ближней зоне соответствует  и справедливо приближенное описание

                                                ,

                                                .

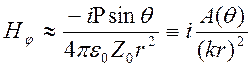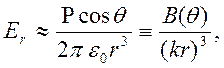
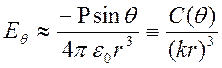В ближней зоне электрическое поле больше, чем магнитное и изменяется оно боле резко с изменением расстояния. Плотности энергии электрического и магнитного полей изменяются по законам

            В дальней зоне  при имеем , и главные компоненты имеют вид

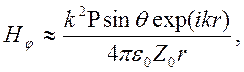
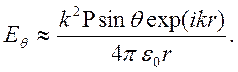
В дальней зоне в каждой точке (локально) поле приближенно имеет вид плоской волны, причем .Поток энергии, переносимый волной направлен по радиусу от источник: . Средний за период поток энергии через единичную площадку на расстоянии  от источника определяется формулой

                                                .

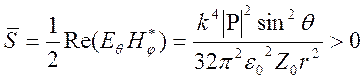Этот же результат получается при использовании строгих формул.

            Полный поток энергии от источника через сферическую поверхность радиуса  будет постоянным:

                        .

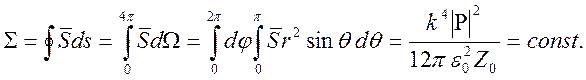
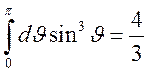Этот результат имеет место как в дальней зоне , так и в ближней зоне.

С другой стороны, этот поток можно представить в виде энергии, выделяемой током  на некотором сопротивлении (его называют сопротивлением излучения антенны):

                                                            .

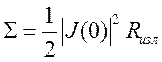По существу это равенство является определением сопротивления излучения антенны. Учитывая, что 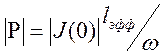, получим

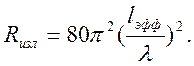
            Исследуем свойства фазовой скорости компоненты поля  Используем представление

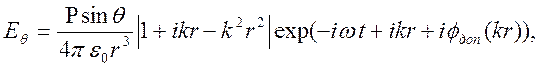
где

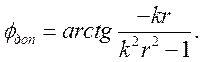
Введем обозначение

                                                .

Фазовая скорость - это скорость перемещения поверхности равной фазы. Уравнение этой поверхности  Фазовая скорость 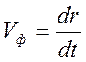 находится из уравнения

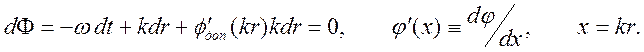
Получаем

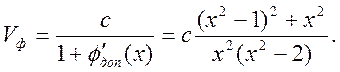
График фазовой скорости показан на Рис.10.14. Фазовая скорость отрицательна при  (напомним, что полный поток энергии  везде положителен и постоянен), в этой области формируется поле излучения. При выполнении условия  фазовая скорость положительна и она стремится к скорости света при .