Поле короткой линейной антенны. Принцип перестановочной двойственности. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией, страница 6

                                    .

На больших по сравнению с размерами источника расстояниях () величину  можно приближенно представить в виде              - угол между векторами . Учитывая это, представим (10.75) в виде        

                       

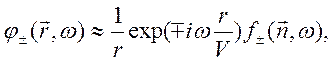
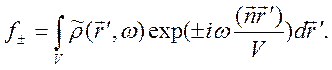
Подстановка этого представления в (10.73) дает

                                    .

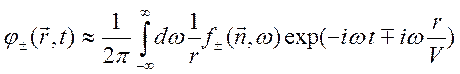Принципу Зоммерфельда удовлетворяет решение , поскольку оно представляет собой суперпозицию волн, уходящих по фазе на бесконечность. Решение  является суперпозицией волн, сходящихся из бесконечности к источнику. В среде без дисперсии одинаковы фазовая, групповая скорости и они совпадают со скоростью переноса энергии. Поэтому  удовлетворяет принципу Мандельштама. Покажем, что  удовлетворяет принципам причинности и погашения. Возьмем представление

                                    .

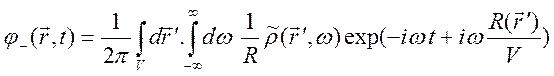Если источник включается  в момент времени  то фурье – образ источника не имеет особых точек в верхней полуплоскости комплексной плоскости . Следовательно, при условии 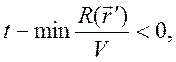 можно замкнуть контур интегрирования по  на бесконечности в верхней полуплоскости. При этом будем иметь , так как в верхней полуплоскости подынтегральная функция не имеет особых точек. Таким образом,  удовлетворяет принципу причинности.

            Учет влияния диссипации приводит к комплексности волнового числа, причем 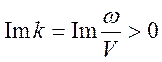. В разложении (10.75) условию погашения на бесконечности удовлетворяет функция . Поэтому  удовлетворяет и принципу погашения. На основе решения этой конкретной задачи, пришли к выводу, что в среде без дисперсии все принципы излучения эквивалентны. Они приводят к отбору одного и того же решения . Ниже будет показано, что этот вывод носит общий характер.

            2). Пусть поле  возбуждается источником конечных размеров в сплошной однородной среде и пусть оно описывается линейным скалярным дифференциальным уравнением

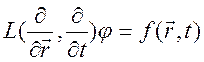                                                ,                                     (10.76)

где  - линейный оператор,  - функция, описывающая источник. Применяя преобразование Фурье, получим алгебраическую систему уравнений для фурье – образов

                                               

При  получается условие существования ненулевых решений (дисперсионное уравнение)

                                                   при .

На основе преобразования Фурье имеем интегральное представление решения, являющегося суперпозицией расходящихся на бесконечность волн (это решение соответствует  для среды без дисперсии)

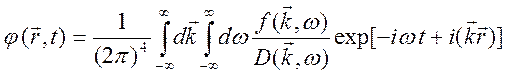                                    .            (10.77)

В среде без потерь функция  будет вещественной, в области прозрачности вещественными будут и корни  дисперсионного уравнения  Следствием этого является расположение полюсов  на вещественной оси  (на пути интегрирования по ). Это обстоятельство приводит к необходимости определить правило обхода этих особых точек. Воспользуемся для этого принципом причинности: . При условии  контур интегрирования по частоте  в (10.77) можно замкнуть на бесконечности в верхней полуплоскости . Чтобы выполнилось условие , внутри замкнутого контура не должно быть особых точек (они лежат на вещественной оси). Поэтому путь интегрирования по частоте должен обходить особые точки сверху, как показано на Рис.10.17. Условие причинности можно удовлетворить также и другим способом: если в выражении  заменить  на . Тогда нули уравнения  сместятся с вещественной оси в нижнюю полуплоскость. Контур интегрирования, проходящий по вещественной оси , при  можно замкнуть на бесконечности в верхней полуплоскости. Внутри этого контура нет особых точек, поэтому получим . Возьмем параметр  малым и воспользуемся приближенным представлением