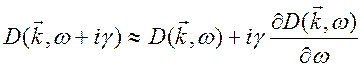Поле короткой линейной антенны. Принцип перестановочной двойственности. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией, страница 7

                                                .

Применим формулу

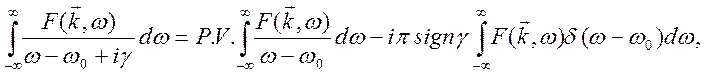                   (10.78)

где 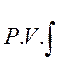означает интеграл в смысле главного значения. В результате (10.77) представим в виде

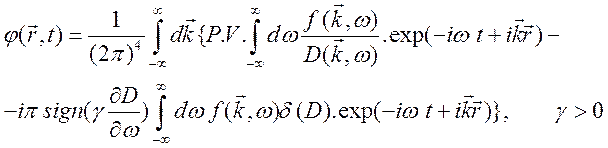.                  (10.79)

Это представление было получено Ю.В. Чугуновым (1969 г.), оно является решением уравнения (10.76). Это решение удовлетворяет принципу причинности.

            Третий способ вычисления интеграла в (10.77) сводится к введению малой мнимой добавки в волновое число, например в  составляющую волнового вектора: . Заранее знак добавки  не известен. Знак  должен выбираться так, чтобы потенциал  удовлетворял принципу причинности. Используем приближенное представление

                                   

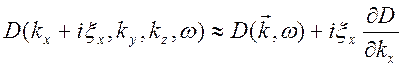
и применяя формулу (10.78), получим

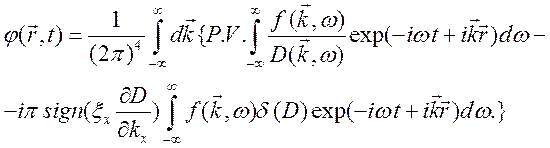.               (10.80)

Условие совпадения формул (10.79) и (10.80):

                                                .

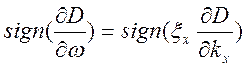Отсюда получаем правило выбора знака добавки

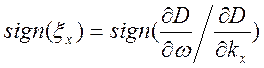                                                .                                       (10.81)

Из условия  получаем  или 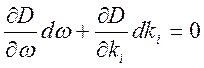. Это означает, что для компонент групповой скорости имеем представление

                                                .

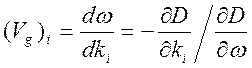Следовательно, условие (10.81) можно представит в виде

                                    .

Аналогичные рассуждения для малых мнимых добавок  к компонентам  приводят к правилу

                                    ,           

Используя эти соотношения, выясним связь между направлением вектора  (радиус – вектор между точками источника и наблюдения) и вектором групповой скорости  в волнах, составляющих поле , которое удовлетворяет принципу причинности. С этой целью рассмотрим входящий в (10.77) интеграл

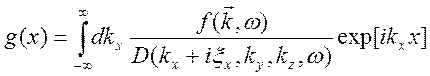                                    .                       (10.82)

При отсутствии потерь  полюсы лежат на вещественной оси , а при  они смещаются с вещественной оси. Замыкая контур интегрирования в (10.82) в верхней полуплоскости на бесконечности при , и в нижней полуплоскости при , имеем

1).           ,        при      ,

               ,        при      ,

2).           ,        при      ,

               ,        при      .

Таким образом, при  вклад в поле  дают волны, у которых выполнены условия . В области   вклад в поле дают волны, обладающие свойством . В обоих случаях эти волны удовлетворяют условию . Рассматривая аналогично интегрирование по , получим следующий результат. Поле , удовлетворяющее принципу причинности, состоит из волн, для которых выполнено неравенство

                                                .

Следовательно, в этих волнах угол между векторами  и  должен быть острым. Именно к такому же условию приводит и принцип Мандельштама: решение  должно строиться на основе волн, уносящих энергию на бесконечность, т.е. удовлетворяющих условию , где  - скорость переноса энергии, или . Это соотношение получается потому, что в средах без потерь скорость переноса энергии монохроматической волны совпадает с групповой скоростью.

            В то же время, в средах с дисперсией векторы  и не параллельны, поэтому в таких средах одновременно могут выполняться условия

                                                 и .

В таком случае использование принципа излучения Зоммерфельда приведет к выбору неправильного решения.

            Можно показать (делать это здесь не будем), что решение, обладающее свойством причинности, удовлетворяет и принципу погашения поля на бесконечности. При этом имеем ограничение на :

                                    .                               (10.83)

Конечно, должно иметь место неравенство .