Поясним
смысл этих условий. Если угол между векторами ![]() и
и ![]() острый, то условию затухания удовлетворяют
волны, уходящие по фазе на бесконечность, в этом случае принцип Зоммерфельда
справедлив. Если же угол между
острый, то условию затухания удовлетворяют
волны, уходящие по фазе на бесконечность, в этом случае принцип Зоммерфельда
справедлив. Если же угол между ![]() и
и ![]() тупой, то в соответствии с (10.84)
затухающими на бесконечности будут волны, у которых
тупой, то в соответствии с (10.84)
затухающими на бесконечности будут волны, у которых ![]() (это
волны приходящие по фазе из бесконечности). В таком случае принцип Зоммерфельда
несправедлив.
(это
волны приходящие по фазе из бесконечности). В таком случае принцип Зоммерфельда
несправедлив.
10.17. Потенциалы Лиенара – Вихерта. Поле движущегося заряда. Дипольное излучение. Релятивистское излучение. Рассмотрим задачу о поле произвольно движущегося в однородной материальной среде без дисперсии точечного заряда.
1). Решение
этой задачи построим, используя выражение для ![]() запаздывающих
потенциалов
запаздывающих
потенциалов
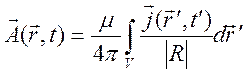 ,
, 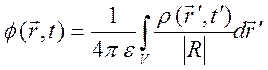 , (10.84)
, (10.84)
где ![]() -
радиус – векторы точек наблюдения и интегрирования соответственно,
-
радиус – векторы точек наблюдения и интегрирования соответственно, ![]() ,
, 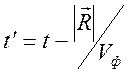 -
время запаздывания, равное времени распространения волны от точки
интегрирования до точки наблюдения,
-
время запаздывания, равное времени распространения волны от точки
интегрирования до точки наблюдения, ![]() - фазовая скорость
волны. Для точечного заряда
- фазовая скорость
волны. Для точечного заряда ![]() , движущегося со
скоростью
, движущегося со
скоростью ![]() , имеем представления
, имеем представления
![]() ,
, ![]() ,
,
где ![]() -
радиус – вектор положения точечного заряда в момент времени
-
радиус – вектор положения точечного заряда в момент времени ![]() . Интегрирование в (10.84) осуществляется в
лабораторной системе координат. Более удобно пользоваться системой координат,
связанной с зарядом. С этой целью введем новую векторную переменную
. Интегрирование в (10.84) осуществляется в
лабораторной системе координат. Более удобно пользоваться системой координат,
связанной с зарядом. С этой целью введем новую векторную переменную
![]()
и представим (10.84) в виде
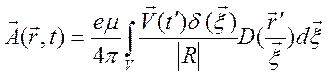 ,
, 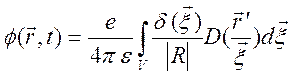 , (10.85)
, (10.85)
где 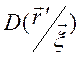 -
якобиан преобразования переменных. Явный вид якобиана можно найти,
воспользовавшись соотношением
-
якобиан преобразования переменных. Явный вид якобиана можно найти,
воспользовавшись соотношением
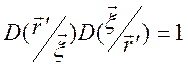 .
.
Элементы определителя  находятся по формуле
находятся по формуле
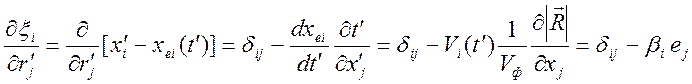 ,
,
где 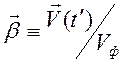 ,
, 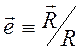 . Якобиан имеет вид
. Якобиан имеет вид
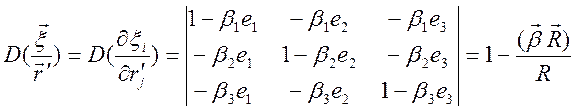 .
.
После интегрирования в (10.85), получим формулы для потенциалов Лиенара - Вихерта
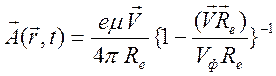 ,
, 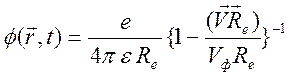 , (10.86)
, (10.86)
где ![]() ,
, ![]() .
.
2). На основе представлений для потенциалов найдем электромагнитное поле, возбуждаемое движущимся зарядом:
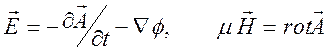 .
.
Дифференцирование в этих формулах
производится по ![]() и
и ![]()
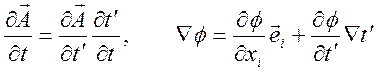 ,
,
где 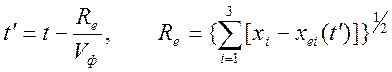 ,
,
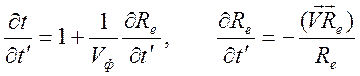 ,
, 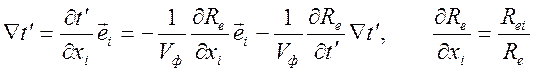 .
.
Из этих формул получаем
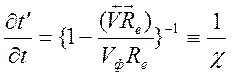 ,
, 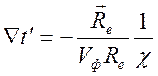 .
.
Учитывая формулы Лиенара – Вихерта (10.86), получим
![]()
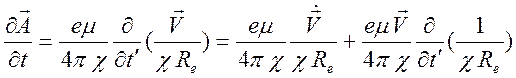 ,
,
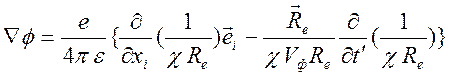
где
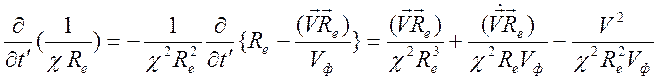 ,
,
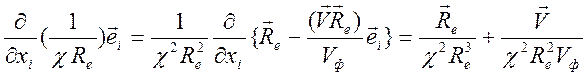 ,
,
после довольно громоздких преобразований получается представление для электрического и магнитного полей
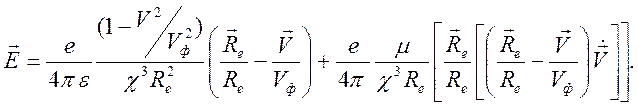
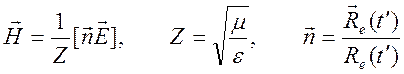 .
.
Отметим характерные закономерности для поля, движущегося точечного заряда
1). При ![]() ,
имеем электростатическое поле заряда:
,
имеем электростатическое поле заряда: 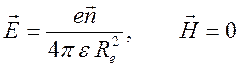 .
.
2). Если скорость движения постоянна, то имеет место закономерность
![]() .
.
3). При ![]() в
дальней зоне имеет место
в
дальней зоне имеет место ![]() .
.
Полный поток энергии от неравномерно движущегося заряда будет отличным от нуля на бесконечности.
4). При ![]() и
и
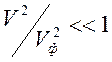 имеет место приближенное описание
имеет место приближенное описание
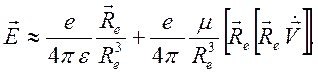 ,
,
В дальней зоне возможно дополнительное упрощение (дипольное излучение)
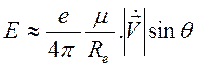 ,
,
где ![]() - угол
между векторами
- угол
между векторами ![]() и
и ![]() . Поле
имеет диаграмму направленности с максимумом при
. Поле
имеет диаграмму направленности с максимумом при ![]() .
.
5). Ультрарелятивистское
излучение при ![]() . Поле имеет резко выраженную
зависимость от угла между векторами
. Поле имеет резко выраженную
зависимость от угла между векторами ![]() и
и ![]() (ниже этот угол обозначен
(ниже этот угол обозначен ![]() ) благодаря множителю
) благодаря множителю ![]() :
:
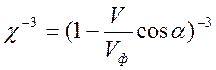 .
.
При ускоренном релятивистском движении заряженной частицы, например, при движении по окружности во внешнем магнитном поле возникает синхротронное (магнитотормозное) излучение.
6). При ![]() возникает
черенковское излучение.
возникает
черенковское излучение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.