Поле короткой линейной антенны. Принцип перестановочной двойственности. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией, страница 4

2. Вопрос о возможных видах волн и об их свойствах можно решить на основе анализа дисперсионного уравнения для плоских волн (фурье – образов полей). Из дисперсионного уравнения находится связь между волновым вектором и частотой. Это позволяет исследовать свойства фазовых и групповых скоростей в зависимости от параметров среды и направления распространения. После преобразования Фурье, однородные уравнения Максвелла можно привести к виду

                                       (10.70)

                       

где . Векторы  и  в плоской волне (фурье - образы) ортогональны волновому вектору. Поле  не обладает этим свойством в анизотропной среде, оно может иметь продольную (вдоль направления ) составляющую. Отметим, что в изотропной среде поле  имеет продольную составляющую только при  (это дисперсионное уравнение продольных волн). Это соотношение является прямым следствием уравнения  при .

Система (10.70) с учетом формулы

                                               

приводится к однородному алгебраическому векторному уравнению для фурье – образа вектора электрического поля

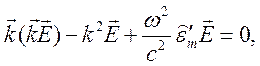                                                                             `(10.70.А)

или

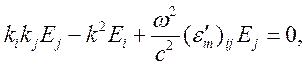
                                 ,                   (10.71)

где ,  - символ Кронекера. Условие существования ненулевого решения возможно при условии равенства нулю определителя системы

                                                .

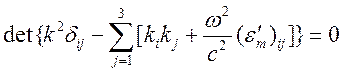Это уравнение и называется дисперсионным.

            3. В частном случае изотропной среды представим вектор электрического поля в виде суммы двух слагаемых , где ,           . Дисперсионное уравнение разбивается на два. В уравнении (10.71.А) имеем  значит дисперсионное уравнение для продольной волны имеет вид

                                                .

Для поперечной волны из (10.70.А) при  следует

                                               

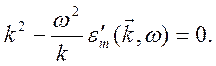
Первое уравнение описывает продольную волну, в ней нет магнитного поля (имеет место уравнение ). Второе уравнение относится к поперечной волне.

            4. Рассмотрим одноосный кристалл. Главную диэлектрическую ось (она совпадает с осью симметрии кристалла, и ее называют оптической осью кристалла) обозначим . Вращением системы координат добьемся того, что вектор  «ляжет» в плоскость :

                                                ,

где  - угол между осью  и волновым вектором . Система алгебраических уравнений (10.71) для фурье – образов поля  имеет вид

                                   

                                   

                                   

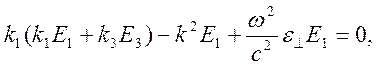
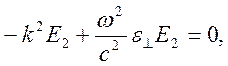
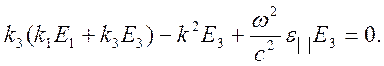
Уравнение для  «отщепляется» от остальной системы. Из него следует дисперсионное уравнение для поперечной электромагнитной волны (обыкновенной волны)  и представление для волнового числа этой волны

                                                            .

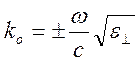В такой волне анизотропия не проявляется.

            Во второй волне (необыкновенной) вектор  имеет как продольную (вдоль оптической оси) так и поперечную компоненты. Эта волна является продольно – поперечной. Компоненты поля описываются системой уравнений

                                               

                                               

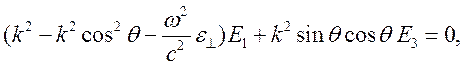
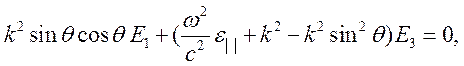
ненулевое решение системы возможно при условии равенства нулю ее определителя. Получаем представление для волнового числа необыкновенной волны

                                                .

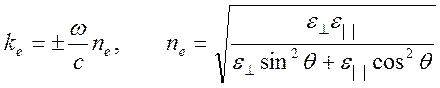Где  - показатель преломления необыкновенной волны, он зависит от угла . Фазовая скорость так же зависит от угла . В предельном случае  необыкновенная волна переходит в обыкновенную волну. Так как показатели преломления обыкновенной и необыкновенной волн различные, то при падении плоской волны из изотропной среды на границу с анизотропной средой, в последней волна «распадается» на обыкновенную и необыкновенную. Они распространяются под разными углами к границе раздела (эффект двойного лучепреломления).