Поле короткой линейной антенны. Принцип перестановочной двойственности. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией, страница 5

10.16. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией. Особенности использования принципа излучения Зоммерфельда для сред с дисперсией. При решении задач о поле, возбуждаемом сторонними источниками в безграничной среде, возникает проблема выбора правильного решения из набора возможных независимых частных решений исходных уравнений. Наибольшие трудности возникают при решении идеализированных задач без учета потерь. Существует несколько различных способов отбора решения, соответствующего физической реальности. Условия, на которых основаны эти способы, часто называются принципами излучения. Известны: принцип Зоммерфельда, принцип Мандельштама, принцип погашения поля на бесконечности и принцип причинности. Они основаны на задании граничных условий на бесконечности для самого поля или для элементарных волн, на основе которых строится это поле, на использовании закона сохранения энергии, на задании начальных условий.

Если решение строится в виде разложения по элементарным волнам, то в соответствии с принципом Зоммерфельда разложение необходимо вести по расходящимся от источника волнам.

            Л.И. Мандельштам (1947) предложил отбирать физически реализуемое решение на основе требования отвода энергии от источника. Вдали от источника поле должно состоять только из волн, которые уносят энергию на бесконечность. Мандельштам отметил, что такой отбор решений важен в средах, имеющих различные знаки групповой и фазовой скоростей вдоль некоторых направлений.

Если излучение распространяется в равновесной среде, то эта среда обладает поглощением (диссипацией), хотя оно иногда бывает и достаточно малым. Это поглощение приводит к затуханию полей при удалении от источника на бесконечность. На этом основано введение бесконечно малых потерь (для облегчения построения решения иногда вводятся некоторые «искусственные» потери) в идеализированных задачах без учета диссипации (например, задача о волнах в вакууме). В построенном таким образом решении потери затем устремляются к нулю. Введение малых потерь делает очевидным отбор правильного решения, но может значительно усложнить решение исходной задачи.

Принцип причинности требует, чтобы поле возникало в некоторой точке при выполнении условия. Это поле создается источником, включаемым в момент времени . Параметр  учитывает запаздывание импульса при распространении его от источника в точку наблюдения с конечной скоростью.

Все принципы исходят из разумных (но различных) предположений. Естественно ожидать, что все эти способы, примененные к решению одной и той же задачи, должны привести к одному и тому же результату. На самом деле это так для полей в средах без дисперсии, но не всегда верно при наличии дисперсии.

            1). Рассмотрим вопрос об эквивалентности различных принципов излучения в среде без дисперсии. В качестве простого примера рассмотрим вопрос о выборе правильного решения волнового уравнения для скалярного потенциала

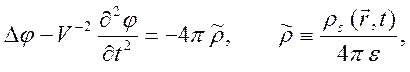                                                                (10.72)

где  - плотность сторонних зарядов,  - фазовая скорость. Этому уравнению удовлетворяют два линейно независимые решения

                                   

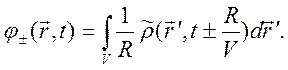
Смысл обозначений ясен из Рис.10.16. Множитель  является функцией Грина уравнения (10.72),  - точка наблюдения. Преобразование Фурье для функций  имеет вид

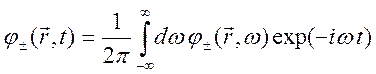                                    ,                             (10.73)

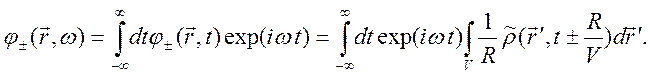                        (10.74)

Введем новую переменную , и меняя порядок интегрирования в (10.74), получим

                                                                     (10.75)

Множитель 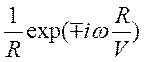 представляет собой функцию Грина для решения уравнения