10.6-А.
Свойства диэлектрической проницаемости и волнового числа. Исследуем зависимость от частоты параметров ![]() и
и ![]() .
.
Для фазовой скорости имеем представление
![]()
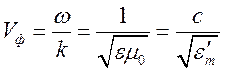 .
.
Функция
![]() связана с относительной комплексной
диэлектрической проницаемостью изотропной среды с пространственной дисперсией
формулой
связана с относительной комплексной
диэлектрической проницаемостью изотропной среды с пространственной дисперсией
формулой
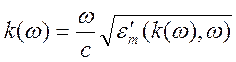 .
.
Имеет
место представление Фурье для процесса, начинающегося в момент времени ![]() (
(![]() при
при ![]() ):
):
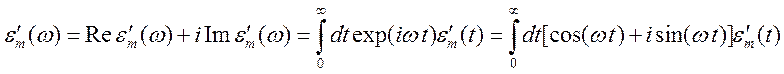 .
.
В
среде без пространственной дисперсии функция ![]() обладает
свойствами:
обладает
свойствами:
![]() .
.
Выше
отмечалось, что любая среда для достаточно высоких частот ведет себя как
вакуум. ![]() В этой области частот, пренебрегая
пространственной дисперсией, воспользуемся разложением
В этой области частот, пренебрегая
пространственной дисперсией, воспользуемся разложением
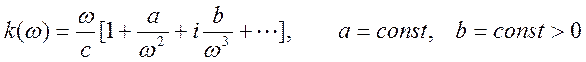 . (10.28)
. (10.28)
В
квадратных скобках формулы (10.28) отсутствует слагаемое вида ![]() . При этом в пределе
. При этом в пределе ![]() имеем
имеем ![]() ,
, ![]() . Если бы в (10.28) присутствовал член
. Если бы в (10.28) присутствовал член ![]() , то имело бы место представление
, то имело бы место представление 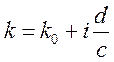 при
при ![]() .
Последнее представление противоречило бы закономерности
.
Последнее представление противоречило бы закономерности ![]() при
при
![]() .
.
10.7.
Распространение переднего фронта нестационарной волны. Интегральное представление одномерного нестационарной
волны, распространяющейся в направлении ![]() и
соответствующей одному из типов волн в однородной среде (
и
соответствующей одному из типов волн в однородной среде (![]() - корень дисперсионного уравнения
- корень дисперсионного уравнения ![]() ). В среде с потерями для такой волны
). В среде с потерями для такой волны ![]() .
.
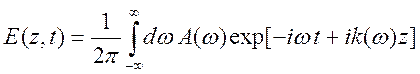 , (10.29)
, (10.29)
Где
функция ![]() имеет передний на уровне
имеет передний на уровне ![]() :
:
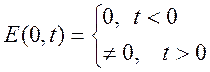 .
.
Согласно (10.29) имеем представление
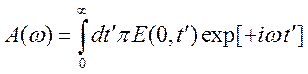 .
.
Особые
точки подынтегральной функции в (10.29) лежат в нижней полуплоскости ![]() . Это обеспечивает выполнение принципа
причинности (поле возникает только после включения источника). Соотношение
(10.29) представляется в виде
. Это обеспечивает выполнение принципа
причинности (поле возникает только после включения источника). Соотношение
(10.29) представляется в виде
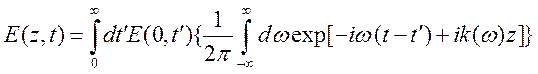 , (10.30)
, (10.30)
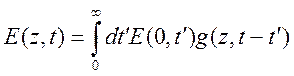 ,
,
Где
![]() называется импульсной функцией:
называется импульсной функцией:
 , (10.31)
, (10.31)
она
обладает свойством ![]() (
(![]() -
дельта функция Дирака).
-
дельта функция Дирака).
Покажем, что импульсная функция удовлетворяет принципу
причинности. Особые точки функции ![]() для
пассивных сред расположены в нижней полуплоскости. Выясним, при каких значениях
аргумента
для
пассивных сред расположены в нижней полуплоскости. Выясним, при каких значениях
аргумента ![]() импульсная функция станет отличной от
нуля. При больших значениях
импульсная функция станет отличной от
нуля. При больших значениях ![]() , в области замыкания
контура интегрирования на бесконечности, можно воспользоваться разложением
(10.28) и будем иметь приближенное представление экспоненты
, в области замыкания
контура интегрирования на бесконечности, можно воспользоваться разложением
(10.28) и будем иметь приближенное представление экспоненты
![]() .
.
Это
представление не используется при вычислении интеграла в (10.31), оно
используется только для определения возможности замыкания контура при ![]() .
.
При
выполнении условия 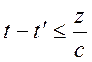 имеется возможность замкнуть контур
интегрирования на бесконечности в верхней полуплоскости
имеется возможность замкнуть контур
интегрирования на бесконечности в верхней полуплоскости ![]() .
Так как внутри такого контура нет особых точек, то
.
Так как внутри такого контура нет особых точек, то
![]() при
при 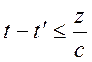 ,
, ![]() . (10.32)
. (10.32)
Если
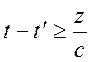 , то можно замыкать контур интегрирования
на бесконечности в нижней полуплоскости
, то можно замыкать контур интегрирования
на бесконечности в нижней полуплоскости ![]() .
Наличие особых точек в нижней полуплоскости обеспечивает
.
Наличие особых точек в нижней полуплоскости обеспечивает
![]() при
при 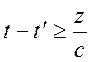 . (10.33)
. (10.33)
Покажем,
что передний фронт нестационарной волны ![]() движется
со скоростью
движется
со скоростью ![]() . Свойства (10.32), (10.33) позволяют поле
. Свойства (10.32), (10.33) позволяют поле ![]() представить в виде
представить в виде
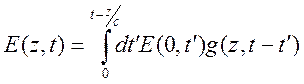 . (10.34)
. (10.34)
Поле
![]() при
при 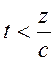 , так
как интегрирование в формуле (10.34) проходит в области отрицательных значений
переменной
, так
как интегрирование в формуле (10.34) проходит в области отрицательных значений
переменной ![]() , где по условию включения
, где по условию включения ![]() . Это соответствует тому, что волновой
процесс, порожденный полем
. Это соответствует тому, что волновой
процесс, порожденный полем ![]() еще не достиг уровня
еще не достиг уровня ![]() . Поле
. Поле ![]() обладает
свойством причинности:
обладает
свойством причинности:
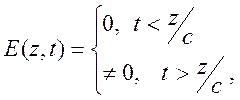 (10.35)
(10.35)
это
свидетельство того, что передний фронт нестационарного поля в любой среде
распространяется со скоростью света в вакууме. Отдельные характерные точки
(нули, максимумы,…) поля могут перемещаться со скоростью большей, чем ![]() , однако они тормозятся при приближении к
фронту и не могут обогнать его.
, однако они тормозятся при приближении к
фронту и не могут обогнать его.
10.8. Теоремы единственности для стационарных задач. Докажем теоремы единственности решения уравнений Максвелла для комплексных амплитуд стационарных полей в неоднородных изотропных средах с потерями. Исходные уравнения для комплексных амплитуд имеют вид
![]() (10.36)
(10.36)
![]() , (10.37)
, (10.37)
где
![]() ,
, ![]() .
Существуют два типа задач: внутренние и внешние.
.
Существуют два типа задач: внутренние и внешние.
В
случае внутренних задач по заданному стороннему току ![]() ищутся
поля
ищутся
поля ![]() внутри объема
внутри объема ![]() (Рис.
10.3). На границе
(Рис.
10.3). На границе ![]() этого объема задаются условия
для касательных составляющих полей
этого объема задаются условия
для касательных составляющих полей
![]()
![]() (10.38)
(10.38)
где
поверхности ![]() и
и ![]() могут
перекрываться. Докажем, что решение системы (10.36), (10.37) с условиями
(10.38) единственно. Для этого допустим, что
могут
перекрываться. Докажем, что решение системы (10.36), (10.37) с условиями
(10.38) единственно. Для этого допустим, что ![]() и
и ![]() два различных решения задачи. Тогда разностное
решение
два различных решения задачи. Тогда разностное
решение ![]() должно удовлетворять системе (10.36),
(10.37) без стороннего источника и это разностное решение удовлетворяет нулевым
граничным условиям
должно удовлетворять системе (10.36),
(10.37) без стороннего источника и это разностное решение удовлетворяет нулевым
граничным условиям
![]()
![]() . (10.39)
. (10.39)
Для этого поля напишем известное энергетическое соотношение
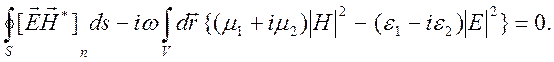
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.