2).
Электрическое поле в падающей волне описывается вектором ![]() , параллельным границе раздела. На границе
раздела составляющая
, параллельным границе раздела. На границе
раздела составляющая ![]() непрерывна. Поэтому в отраженной
и преломленной волнах вектор электрического поля сохраняет ориентацию
непрерывна. Поэтому в отраженной
и преломленной волнах вектор электрического поля сохраняет ориентацию ![]() (в анизотропных средах это не так).
(в анизотропных средах это не так).
3). Считается, что отраженная и преломленная волны остаются плоскими
Использование таких допущений позволяет построить решение, оно единственно согласно соответствующей теореме.
Сначала
рассмотрим ситуацию №1. На границе раздела сред ![]() тангенциальная
составляющая поля
тангенциальная
составляющая поля ![]() должна быть непрерывна:
должна быть непрерывна:
![]() . (10.40)
. (10.40)
Это
условие должно быть выполнено при любых значениях ![]() , а это
приводит к условию равенства показателей экспонент
, а это
приводит к условию равенства показателей экспонент
![]() . (10.41)
. (10.41)
Из (10.40), (10.41) следует
![]() . (10.42)
. (10.42)
Равенство
(10.41) – это закон Снеллиуса. Из (10.41) следует, что ![]() .
Для однозначного выбора
.
Для однозначного выбора ![]() необходимо привлечь
условие убывания отраженного поля при
необходимо привлечь
условие убывания отраженного поля при ![]() . Это
требование выполняется при
. Это
требование выполняется при ![]() . В результате получаем
. В результате получаем
![]() . На Рис.10.5 введен угол
. На Рис.10.5 введен угол ![]() . Из закона Снеллиуса получаем
представление для угла преломления
. Из закона Снеллиуса получаем
представление для угла преломления
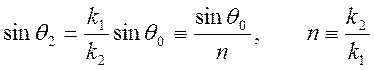 .
.
Если
![]() - вещественный и
- вещественный и ![]() ,
то тогда
,
то тогда ![]() , т.е. нормаль к поверхности равной фазы
преломленной волны «прижимается» к вертикальной оси
, т.е. нормаль к поверхности равной фазы
преломленной волны «прижимается» к вертикальной оси ![]() . При
. При ![]() угол
угол ![]() может
быть комплексным при
может
быть комплексным при ![]() . Если
. Если ![]() -
комплексное число, то
-
комплексное число, то ![]() и
и ![]() принимают
комплексные значения. При этом , в соответствии с условием затухания
преломленной волны при
принимают
комплексные значения. При этом , в соответствии с условием затухания
преломленной волны при ![]() должно выполняться условие
должно выполняться условие ![]()
Для
того, чтобы найти явный вид коэффициентов ![]() нужно
кроме (10.42) получить еще одно условие. Для этого используем граничное условие
нужно
кроме (10.42) получить еще одно условие. Для этого используем граничное условие
![]() (10.43)
(10.43)
для тангенциальных компонент магнитного поля при отсутствии поверхностных токов. Используем уравнение
![]() ,
,
которое для горизонтальной поляризации имеет вид
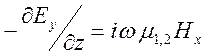 .
.
Отсюда получаем представления полей падающего, отраженного и преломленного:
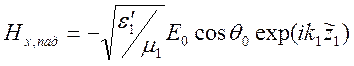 ,
,
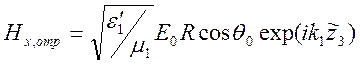 ,
,
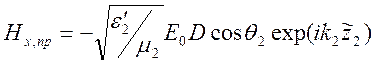 .
.
Из граничного условия (10.43) получаем
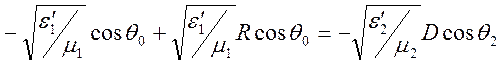 ,
,
которое
совместно с условием (10.42) позволяет определить коэффициенты ![]() для волны горизонтальной поляризации
для волны горизонтальной поляризации
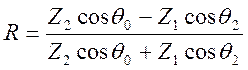 ,
,
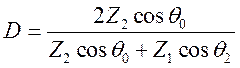 ,
,
где
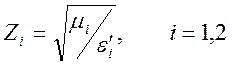 .
. ![]() - характеристические
импедансы (волновые сопротивления) сред.
- характеристические
импедансы (волновые сопротивления) сред.
В случае волны вертикальной поляризации задача решается аналогично, получается:
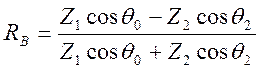 ,
,
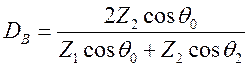 .
.
Рассмотрим некоторые предельные случаи для задачи о волне горизонтальной поляризации.
1.
При отражении волны от оптически
более плотной среды, когда выполняются условия ![]() получаем
получаем
![]() . В этом случае на границе
. В этом случае на границе ![]() имеем «узел» напряженности электрического
поля:
имеем «узел» напряженности электрического
поля: ![]() Такая ситуация наблюдается при отражении от
металла.
Такая ситуация наблюдается при отражении от
металла.
2.
Отражение волны от менее плотной
среды. Будем считать, что ![]() ,
, 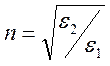 <1. Из закона Снеллиуса следует, что
вещественным угол
<1. Из закона Снеллиуса следует, что
вещественным угол ![]() будет только при выполнении
условия
будет только при выполнении
условия ![]() , где
, где ![]() При
При ![]() наступает полное внутреннее отражение
от оптически менее плотной среды. В этом случае
наступает полное внутреннее отражение
от оптически менее плотной среды. В этом случае ![]() ,
поэтому
,
поэтому ![]() - чисто мнимая величина. В результате
преломленная волна в среде
- чисто мнимая величина. В результате
преломленная волна в среде ![]() будет экспоненциально
затухать при отходе от границы раздела:
будет экспоненциально
затухать при отходе от границы раздела:
![]()
Коэффициенты ![]() представляются в виде
представляются в виде
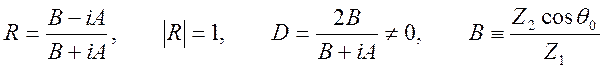 ,
,
следовательно, при полном внутреннем отражении электрическое поле имеет
структуру поверхностной волны: она является распространяющейся вдоль оси
![]() , а с увеличением расстояния от границы
амплитуда поля экспоненциально убывает. Глубина проникновения
, а с увеличением расстояния от границы
амплитуда поля экспоненциально убывает. Глубина проникновения ![]() волны в среду
волны в среду ![]() имеет
вид
имеет
вид
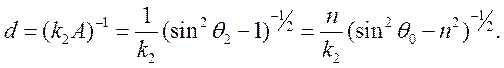
При
учете представлений 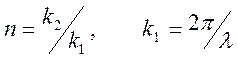 , получаем
, получаем
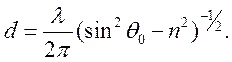
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.