Свойства диэлектрической проницаемости и волнового числа. Распространение переднего фронта нестационарной волны, страница 2

Следствием условия (10.39) является , поэтому имеем

                        .

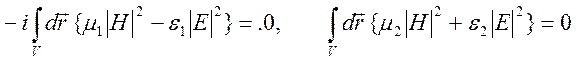В среде с потерями это равенство выполняется только при условии , что и доказывает единственность решения внутренней задачи. В среде без потерь однозначности решения не будет, так как возможно выполнение равенства

                                   

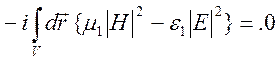
при .

            В случае внешних задач электродинамики ищется решение системы (10.36), (10.37) вне некоторых объемов (Рис.10.4), на поверхности которых задаются граничные условия

                                         

Внешнюю задачу можно свести к внутренней задаче, если ввести поверхность  бесконечно большого радиуса. На поверхности  задается граничное условие

                                                           

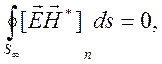
которое называется условием излучения. Это условие в средах с потерями выполняется за счет экспоненциального убывания полей. Доказательство утверждения единственности внешней задачи далее проводится так же как и для внутренних задач. При решении задач в средах без потерь можно ввести малые потери, построить решение, а затем в этом решении сделать предельный переход к среде без потерь.

10.9. Отражение плоских волн от плоской границы раздела. В однородной и безграничной среде могут распространяться плоские монохроматические волны. Если среда неоднородна, то монохроматические волны в ней, вообще говоря, уже не являются плоскими. Существует важный случай, когда и в неоднородной среде могут распространяться плоские монохроматические волны. Это случай двух однородных полу - бесконечных сред, соприкасающихся вдоль плоской границы. Рассмотрим такой случай.

            Плоские волны удовлетворяют уравнениям Максвелла внутри каждого из полупространств, заполненных однородной средой с параметрами  и  (Рис.10.5). Поэтому вопрос сводится к тому, как удовлетворить граничным условиям на поверхности раздела сред и на бесконечности. Пусть плоская волна падает на границу из среды  под углом  к вертикальной оси  В среде  появляется отраженная волна , которая идет в направлении  под углом  к оси  В среде  возникает преломленная волна, идущая в направлении  под углом  к оси  На Рис.10.5 сплошными линиями изображена ситуация (ниже этот случай назовем ситуация №1),когда в среде  компонента вектора фазовой скорости  имеет тот же знак, что и компонента вектора скорости переноса энергии . В этом случае энергия переносится в область  волной, уходящей в сторону . Однако существуют среды, у которых  (назовем этот случай ситуацией №2). В этом случае волна, уносящая энергию в область , должна приходить по фазе из области  к границе раздела сред. Эта волна на Рис.10.5 изображена пунктирными стрелочками.

Плоскую электромагнитную волну можно разбить на две волны в олны с разной поляризацией), распространяющиеся независимо друг от друга. Введем понятие плоскость падения волны как плоскость , проходящую через ось  и через вектор,  характеризующий направление распространения падающей плоской волны. Ось  проведем в плоскости падения (ось  перпендикулярна плоскости падения). Волной вертикальной поляризации назовем волну, у которой . Волна горизонтальной поляризации имеет . Коэффициенты отражения и преломления (прохождения) этих волн различаются. Рассмотрим подробно задачу о волне горизонтальной поляризации.

            Электрическое поле падающей волны запишем в виде

                                                ,

где ,  - волновое число в первой среде,  . Отраженную от границы волну опишем соотношением

                                                ,

где  - коэффициент отражения волны горизонтальной поляризации, ,   . Во второй среде будет преломленная волна

                                                ,

где  - коэффициент преломления, .

На Рис.10.5вектор  для ситуаций №1 и№2 изображен соответственно сплошной и пунктирной линиями.

При написании представлений для отраженной и преломленной волн использованы соображения:

1). Поскольку падающее поле не зависит от координаты ,свойства среды также не зависят от , то отраженная и преломленная волны не зависят от этой координаты.