2).
Фронт падающей волны не плоский, но отличие от плоской волны слабое. Рассмотрим
поле точечного источника (Рис.10.8). Пусть ![]() -
расстояние от источника до участка
-
расстояние от источника до участка ![]() , где рассматриваются
граничные условия. Если
, где рассматриваются
граничные условия. Если ![]() , то фронт волны почти
плоский. Если дополнительно справедливо
, то фронт волны почти
плоский. Если дополнительно справедливо ![]() , то на
участке
, то на
участке ![]() во второй среде волна пойдет почти
перпендикулярно к границе. Таким образом, на участке
во второй среде волна пойдет почти
перпендикулярно к границе. Таким образом, на участке ![]() при
при
![]() амплитуда поля на границе почти постоянна
и выполняются условия применимости для использования (10.44).
амплитуда поля на границе почти постоянна
и выполняются условия применимости для использования (10.44).
10.11. Потенциалы в электродинамике.
1. Часто при решении задач электродинамики, оказывается, удобно перейти от рассмотрения полей к исследованию вспомогательных функций – векторному и скалярному потенциалам. Возьмем уравнения Максвелла в форме
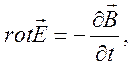 (10.45)
(10.45)
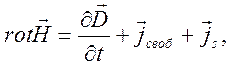 (10.46)
(10.46)
![]() (10.47)
(10.47)
![]() (10.48)
(10.48)
Векторный
потенциал ![]() вводится на основе (10.47) определением
вводится на основе (10.47) определением ![]() . Из (10.45) получаем
. Из (10.45) получаем
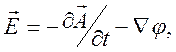 (10.48А)
(10.48А)
где
![]() произвольная функция координат и времени.
Для сред без дисперсии, когда
произвольная функция координат и времени.
Для сред без дисперсии, когда ![]() ,
, ![]() , уравнение (10.46) приводится к виду
, уравнение (10.46) приводится к виду
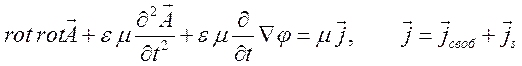 .
.
Или
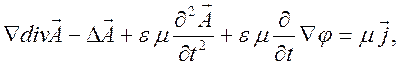 . (10.49)
. (10.49)
Учитывая
произвольность функции ![]() , можно выбрать ее на основе
условия, называемого калибровкой Лоренца:
, можно выбрать ее на основе
условия, называемого калибровкой Лоренца:
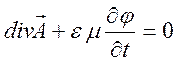 ,
,
тогда (10.49) приводится к уравнению для векторного потенциала
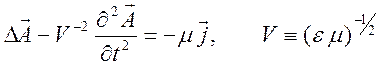 . (10.50)
. (10.50)
Используя уравнение (10.48) и условие калибровки Лоренца, получим уравнение для скалярного потенциала
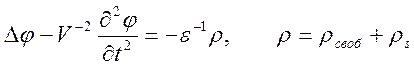 . (10.51)
. (10.51)
![]() Для комплексных амплитуд гармонических
полей получаются равнения
Для комплексных амплитуд гармонических
полей получаются равнения
![]() (10.52)
(10.52)
![]() (10.53)
(10.53)
где
![]() - волновое число. Уравнения (10.50),
(10.51) применимы для сред без дисперсии. Уравнения (10.52), (10.53) описывают
не сами поля, а только их комплексные амплитуды (они также описывают фурье –
образы полей), применимы эти уравнения для сред с временной (частотной)
дисперсией при
- волновое число. Уравнения (10.50),
(10.51) применимы для сред без дисперсии. Уравнения (10.52), (10.53) описывают
не сами поля, а только их комплексные амплитуды (они также описывают фурье –
образы полей), применимы эти уравнения для сред с временной (частотной)
дисперсией при ![]()
![]() , но
при отсутствии пространственной дисперсии.
, но
при отсутствии пространственной дисперсии.
2. Вместо калибровки Лоренца можно использовать другую калибровку.
На основе (10.48) и (10.48А) для среды без дисперсии имеем
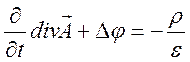 . (10.53.А)
. (10.53.А)
Потенциал
![]() выберем так, чтобы имело место уравнение
электростатики
выберем так, чтобы имело место уравнение
электростатики
![]() (10.54)
(10.54)
При этом калибровка Кулона следует из (10.53.А)
![]() , (10.55)
, (10.55)
при этом получается следующее уравнение для векторного потенциала
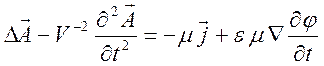 , (10.56)
, (10.56)
В
уравнения для потенциалов (10.50), (10.51) и (10.54), (10.56) входят
дополнительные неизвестные функции ![]() . Для замыкания системы
необходимы уравнения, описывающие
. Для замыкания системы
необходимы уравнения, описывающие ![]() .
.
3. Вместо уравнений (10.46), (10.48) можно использовать другую их эквивалентную форму
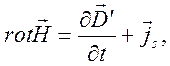
![]()
Для
изотропных сред без дисперсии имеется локальная алгебраическая связь ![]() . В такой ситуации уравнения для
потенциалов с калибровкой Лоренца имеют вид
. В такой ситуации уравнения для
потенциалов с калибровкой Лоренца имеют вид
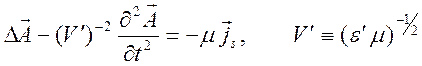 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.