Свойства диэлектрической проницаемости и волнового числа. Распространение переднего фронта нестационарной волны, страница 4

При  глубина проникновения , но с ростом  она уменьшается.

            В заключение рассмотрим вопрос о среднем за период потоке энергии во второй среде при условии полного внутреннего отражения. В преломленной волне горизонтальной поляризации имеется электрическое поле  и две компоненты магнитного поля , которые найдем из уравнения . Имеем:

                                   

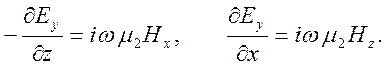
Получаем представления

            .         .

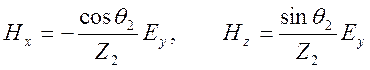Вектор Пойнтинга  имеет две компоненты: . Средний за период поток энергии определяется в виде

   .

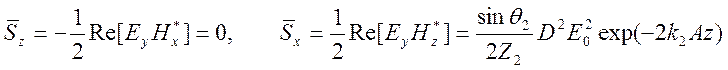Таким образом, поток энергии во второй среде при полном внутреннем отражении направлен вдоль границы (Рис.10.6) и он убывает по мере удаления от границы по закону . Так выглядит явление при отсутствии потерь во второй среде. Учет потерь приведет к тому, что . Для выяснения динамики установления такой специфической картины распределения потока энергии, необходимо решать нестационарную задачу.

Аналогично рассматривается ситуация №2, угол преломления при этом равен . Формулы для коэффициентов отражения и преломления здесь не приводим.

10.10. Приближенные граничные условия Леонтовича. Поверхностный импеданс. Для того чтобы решить задачи электродинамики при наличии границ раздела и найти поле в одной из этих сред, необходимо найти поля во всех средах, учитывая граничные условия. Имеются ситуации, когда допустимо приближенное нахождение поля с использованием приближенных граничных условий Леонтовича для искомого поля. При таком подходе задача существенно упрощается, так как определяется поле только в одной среде. Этот способ оказывается применим, если среда, в которой ищется поле, граничит с хорошо проводящей средой, имеющей большой (по абсолютной величине) показатель преломления.

            Рассмотрим простейшую ситуацию: наличие плоской границы раздела между двумя полу пространствами с различными свойствами (рис.10.7). Пусть среда  имеет свойства вакуума  а в среде  токи проводимости преобладают над токами смещения:  и при этом выполнено неравенство 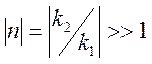. Для плоской волны по закону преломления Снеллиуса при  следует: . Таким образом, при любом угле падения  волна во второй среде идет почти перпендикулярно к границе. Для волны горизонтальной поляризации во второй среде будем иметь

                                   

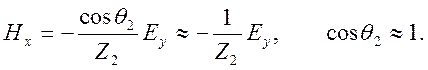
Так как тангенциальные составляющие поля непрерывны на границе, то аналогичная связь должна быть и в первой среде при :

                                                .

Проведя аналогичные рассуждения для плоской волны вертикальной поляризации, придем к граничному условию

                                                .

Таким образом, получен приближенная связь между тангенциальными составляющими поля в первой среде на границе раздела, однако, в эту связь входят свойства второй среды – поверхностный импеданс  Оба условия записываются в виде единой формы

                                                ,                                       (10.44)

где  - внешняя к первой среде единичная нормаль на границе.

Условия (10.44) являются приближенными граничными условиями Леонтовича (1948 г.) Для плоской волны точность этого условия повышается, при выполнении условия . При нормальном падении волны на плоскую границу раздела, условие Леонтовича становится точным.

            Условие  соответствует тому, что

                                                .

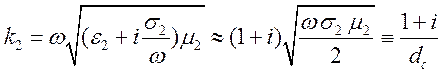Значит, поле во второй среде экспоненциально затухает при увеличении расстояния

                                                .

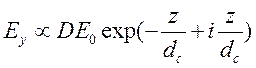При выполнении условия  поле проникает во вторую среду на глубину скин – слоя . Неравенство 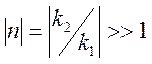обеспечивает малость угла преломления  при любых углах падения .

Большое значение условий Леонтовича заключается в том, что их можно применять при решении более сложных задач электродинамики. Рассмотрим условие их применимости в некоторых из этих случаев.

            1). Если вторая оптически более плотная среда неоднородна, но неоднородность ее проявляется при , то в условии (10.44) такая неоднородность не проявится существенным образом. Если неоднородность среды проявляется уже при , но свойства каждого слоя удовлетворяют условию , , то и в этом случае применимо условие Леонтовича, но с импедансом , зависящем от свойств этих слоев.