Свойства диэлектрической проницаемости и волнового числа. Распространение переднего фронта нестационарной волны, страница 6

                                               

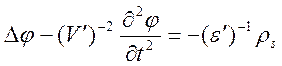
а с калибровкой Кулона они принимают форму

                                               

                                                .

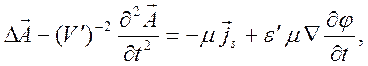
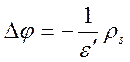4.  Для сред с параметрами  можно ввести векторный потенциал Герца  с помощью соотношения

                                                .

При этом удовлетворяется калибровка Лоренца, если взять следующее представление для

                                                .

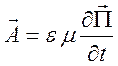Учитывая       связи между полями

                                               

                                       ,

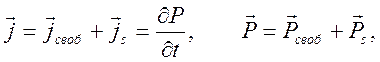
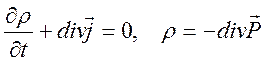из (10.50) и (10.51) получим систему уравнений

                                   

                                   

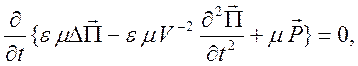
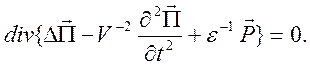
Эта система будет выполнена, если вектор Герца удовлетворяет уравнению

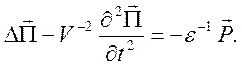                                                                                (10.57)

Если потенциал Герца определен, то электромагнитное поле находится с помощью операции дифференцирования:

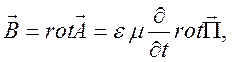                                                                                 (10.58)

                                   

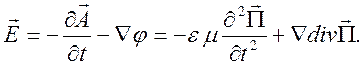
Учитывая уравнение (10.57) и соотношение , получим представление

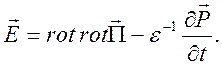                                                                                   (10.59)

В формулах (10.58), (10.59) поля выражаются через вектор Герца с помощью операции . Это означает, что новый вектор  (здесь  - произвольная функция) не меняет поля  (вектор Герца обладает свойством градиентной инвариантности). Это свойство вектора Герца позволяет проводить дополнительное упрощение вычислений. В случае сред с временной дисперсией, но без пространственной дисперсии, возможно рассмотрение комплексных амплитуд для потенциалов. Для них получаются соответствующие уравнения при замене , .

10.12. Поле точечного и пространственно распределенного источников в однородной среде без дисперсии. Исследуем поле, возбуждаемое точечным нестационарным источником в виде заряда, плотность которого описывается функцией

                                                .

В сферической системе координат .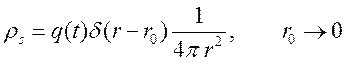

Волновое уравнение для скалярного потенциала имеет вид

                                               

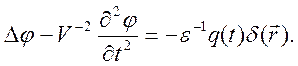
Задача обладает сферической симметрией, поэтому можно использовать однокомпонентный вектор Герца , который удовлетворяет уравнению

                                               

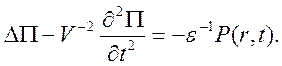
В сферической системе координат, вне источника () уравнение для скалярного потенциала имеет вид

                                    .

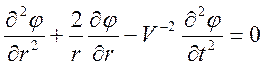С помощью введения новой неизвестной функции  можно избавиться от первой производной по радиальной координате:

                                    .

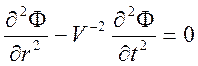Общее решение этого уравнения имеет вид суммы двух произвольных функций

                                    ,

где  описывает волну, распространяющуюся в направлении , а функция  описывает волну, приходящую из бесконечности. Мы решаем задачу о возбуждении поля локализованным источником. Это поле должно быть волной «расходящейся»:

                                    .

В случае статики  и имеем закон Кулона

                                   

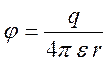
Можно показать (это делается в курсе математической физики), что при  имеет место представление

                                                .

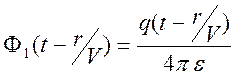Получаем выражение для скалярного потенциала

                                                            .

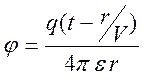Аналогично получается представление

                                                            .

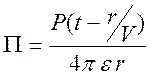При непрерывном распределении заряда (Рис.10.9) в силу принципа линейной суперпозиции потенциал такого объемного заряда можно представить в виде интеграла

                                    .

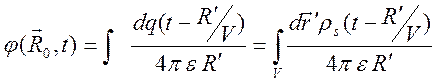Интегрирование производится по объему, занимаемому распределенным источником,  - точка наблюдения. Аналогично выглядит и решение для потенциала Герца

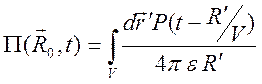                                                .                           (10.60)