Лавинно-стримерный переход. Структура стримера. Головка стримера. Катодонаправленный и анодонаправленный стримеры при импульсном воздействии напряжения, страница 8

                                           

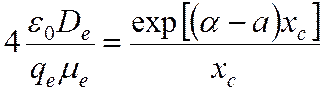
Это уравнение на x_c. Координата лавины связана с числом электронов соотношением (1). Применим его и получим уравнение на N_e. Оно позволяет определить, при каком числе электронов в лавине произойдет лавинно-стримерный переход.

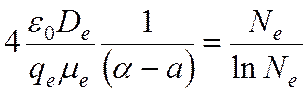                                                        (77)

Мы видим по соотношению (77), что число электронов, при котором происходит лавинно-стримерый переход, зависит лишь от сорта газа и его концентрации  - этими параметрами определяется значение коэффициентов ионизации и прилипания, диффузии и подвижности. Зависимости от напряженности поля нет. Более того, оказывается для разных газов значение критического числа электронов близко и составляет порядка 10⁸. Этим критерием обычно пользуются, и при существующей точности измерений такой простой критерий дает такие же результаты, как расчет по формуле (77). Итак, простой критерий перехода:

                                                        

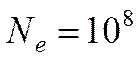
Продемонстрируем применение критерия для однородного поля в азоте и в сухом воздухе:

кВ/см	α, 1/см		Расстояние от старта лавины до точки перехода в стример, см
	Азот	Воздух	Азот	Воздух
20	0.25		73
30	6.3	8.1	2.9	2.3
50	102	96	0.18	0.19
70	337	314	0.054	0.059
90	656	656	0.028	0.028
100	828	873	0.022	0.021

Критерий перехода в неоднородном поле.

Метод расчета точки лавинно-стримерного перехода обобщается на случай неоднородного поля. Для этого предположим, что характерный масштаб изменения поля гораздо больше характерных размеров лавины. Тогда формулы (1) и (33) переходят в следующие выражения:

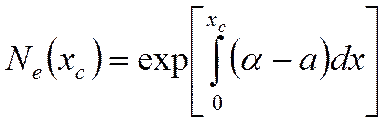                                             (88)

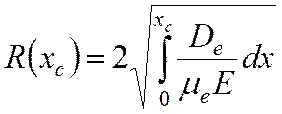                                                            (99)

Начиная интегрирование от поверхности электрода, его ведут вдоль силовой линии электрического поля. В каждой точке x_c мы можем характерное поле лавины по формуле (66) и сравнить его со значением внешнего поля в данной точке. Методика такого расчета иллюстрируется графиком на рисунке 128.

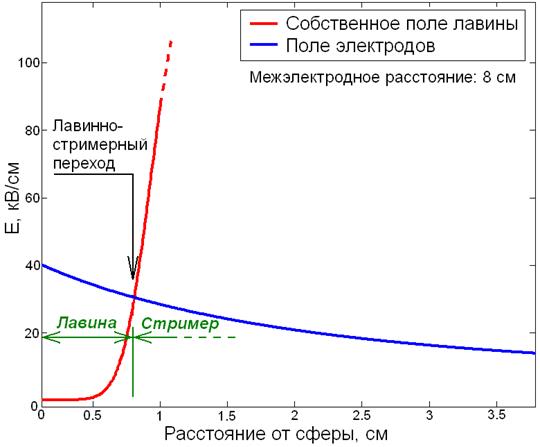
Рисунок 128. Расчет точки лавинно-стримерного перехода в системе электродов сфера-плоскость. Напряжение 135 кВ, радиус сферы 44 мм, межэлектродное расстояние 8 см.

При расчете лавинно-стримерного перехода в неоднородном поле также с успехом применяется упрощенный критерий, поскольку собственное поле лавины растет экспоенциально и меняется по мере продвижения лавины гораздо быстрее, чем внешнее поле. Упрощенный критерий лавинно-стримерного перехода – число электронов в лавине достигает 10⁸:

                                                        

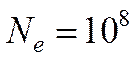
Расчет числа электронов требует интегрирования по формуле (88).

Динамика стримера в неоднородном поле.

Формула (6), хотя и является приближенной, и к тому же выведенной для случая однородного поля, все же позволяет сделать некоторые важные выводы о движении стримера. Так, запишем производную от собственной напряженности поля лавины:

                                                 

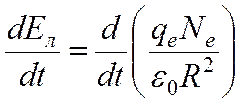
Вместо переменной времени t мы можем использовать координату центра лавины x и интересоваться производной:

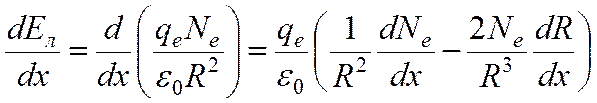                                                                                      (10)

Как видно, при развитии лавины есть два противоборствующих процесса – рост числа электронов способствует увеличению напряженности поля, а рост характерного радиуса (из-за диффузии) снижает напряженность.