В начальный момент времени задан компактный пакет электронов. Это достигается заданием высокой (1016 1/м3) концентрации электронов в небольшой (радиус 10 мкм, длина 20 мкм) цилиндрической области, удаленной от анода. В остальной области задается нулевая концентрация электронов 0 1/м3.
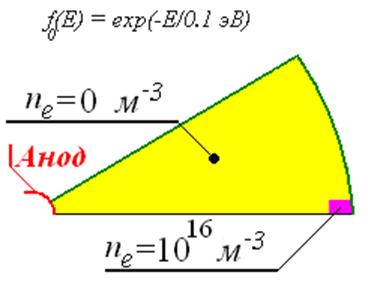
Рисунок 29. Начальные условия в задаче.
Электроны могут свободно проникать через границы модели, другие частицы – нет. Учитывая малые времена расчета, то, что ионы не нейтрализуются на границе, не должно повлиять на решение – они просто не успеют туда прийти.
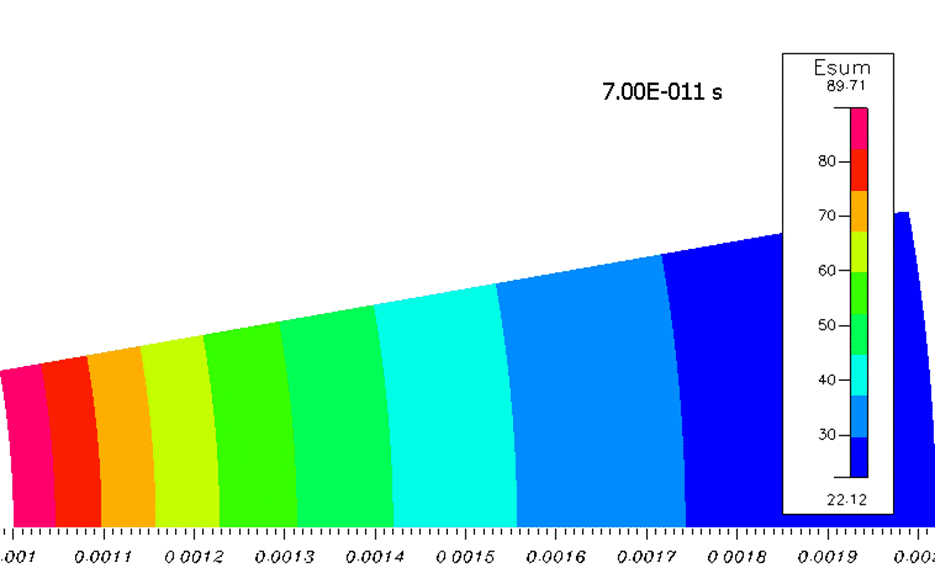
Рисунок 1. Распределение напряженности поля на начальном этапе, когда объемный заряд вносит пренебрежимо малое искажение.
На начальном этапе распространение облака электронов происходит качественно как в классической лавине. Концентрация электронов расплывается вследствие диффузии, размножения почти нет (рисунок 2).
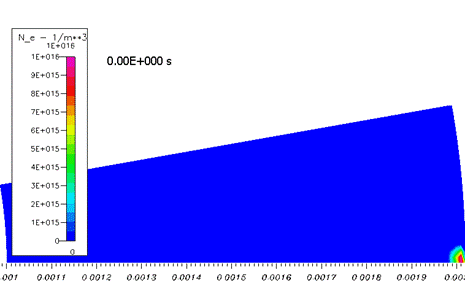
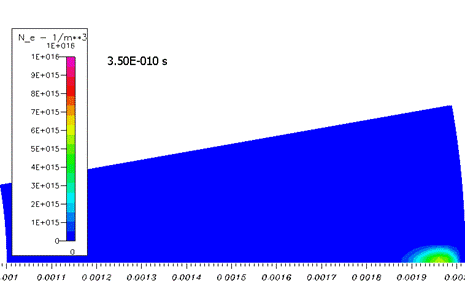
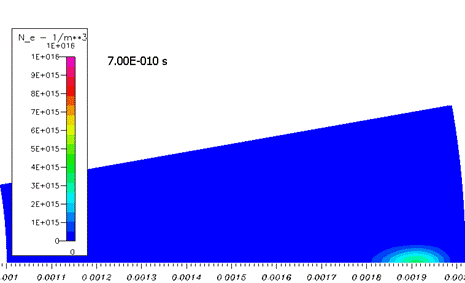
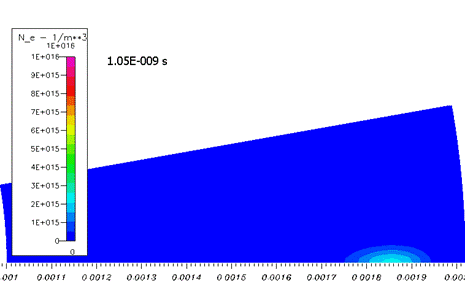
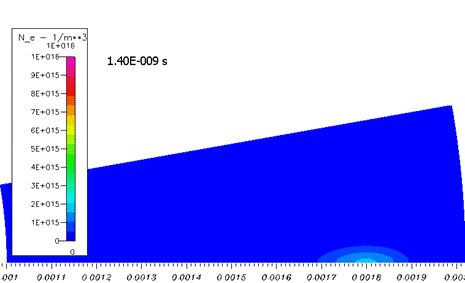
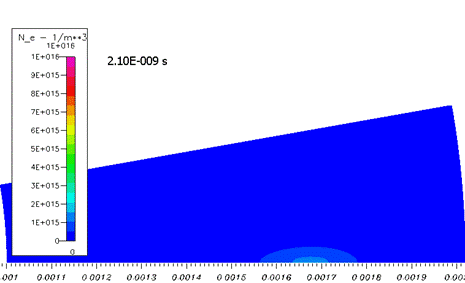
Рисунок 2. Развитие системы на начальном этапе – «простая лавина». 0-2,5 нс. Концентрация электронов. Пределы шкалы на всех графиках одинаковая.
Собственно, на этом этапе нет лавинного процесса. В азоте нет прилипания, поэтому критерием наличия лавинного процесса можно принять условие:
![]()
Здесь α – коэффициент ионизации, Δx – длина участка, который проходит электронное облако. В нашем случае Δx = 1 мм, поэтому о лавине можно говорить, когда коэффициент ионизации превышает α = 1000 1/м – иначе на всей длине участка электрон испытает в среднем менее 1 столкновения, то есть размножения почти не будет. По опытным данным это значение коэффициента ионизации соответствует напряженности 32 кВ/см. То есть до этой напряженности в нашей системе мы имеем не лавину, а распространяющееся облако электронов, число которых остается постоянным.
Значение напряженности 32 кВ/см соответствует расстоянию примерно 0,7 мм от сферы, ближе начинается лавинный процесс.
В момент времени 3 нс концентрация электронов у поверхности сферы сравнялась с концентрацией электронов в максимуме лавины, дальше максимум концентрации находится уже у поверхности сферы. Два локальных максимума соединяет перемычка.
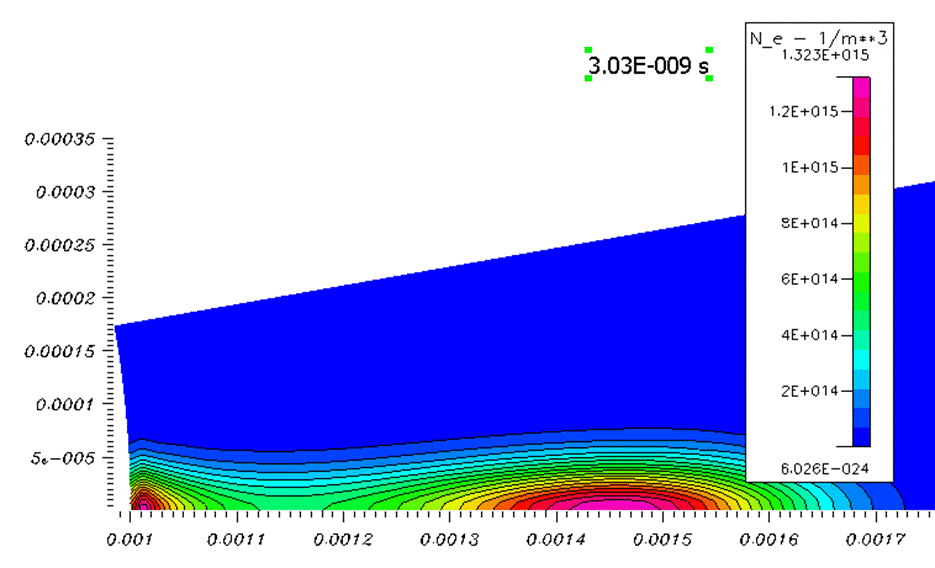
Рисунок 3. Концентрация электронов в момент времени 3,03 нс. Максимумов концентрации два – в центре лавины и у сферического электрода.
Прежде чем говорить о природе максимума, отмечу, что хотя характерный радиус лавины небольшой – около 0,05 мм, значительная концентрация электронов наблюдается по всей модели, хотя она, конечно, на несколько порядков меньше концентрации электронов в максимуме лавины (рисунок 4).
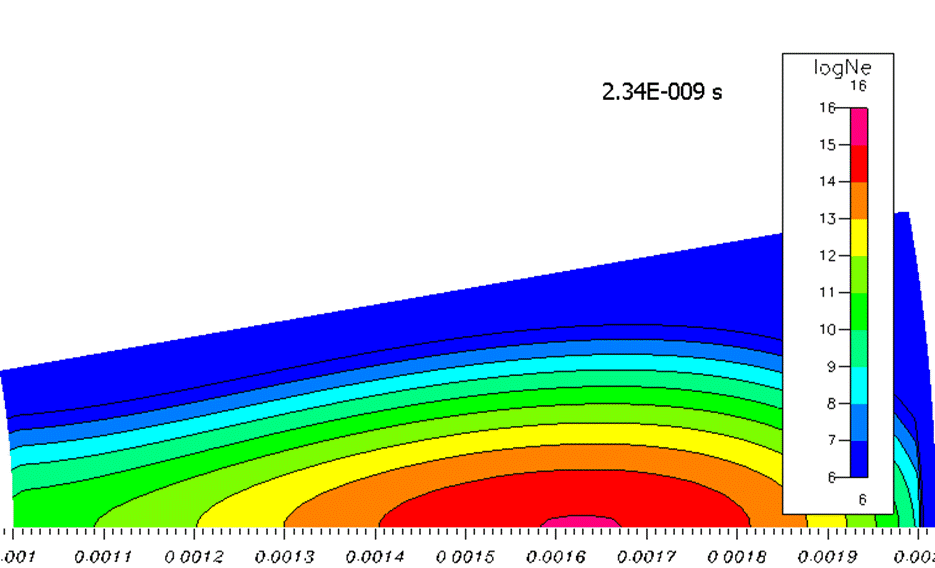
Рисунок 4. Логарифмический график концентрации электронов. Хотя центр лавины прошел всего 35% длины модели, у сферы наблюдается концентрация электронов до 1011 1/м3.
Это свойство уравнения диффузии, которым обладает и уравнение на ФРЭЭ – концентрация частиц появляется мгновенно во всей области, хотя она и на много порядков меньше концентрации в центре облака. Есть ли физический смысл в таком «мгновенном» распространении? Облако электронов расплывается, поскольку движение электронов хаотическое. Центр лавины движется с дрейфовой скоростью электронов, однако их реальная скорость намного выше. В нашей системе встречаются электроны с энергий 10 эВ и выше, хотя их и мало. Этой энергии соответствует скорость – 1,9·106 м/с. Расстояние в 1 мм по прямой такой электрон способен пройти за 0,5 нс. Разумеется, вероятность такого события ничтожно мала, поскольку на этом пути электрон должен много раз упруго удариться о молекулы, малость этой вероятности и описывается гауссовой экспонентой. Но утверждение, что малая доля электронов может по скорости опередить центр лавины на порядок – вполне физично. Это возможно благодаря тому, что тепловая скорость электронов не менее чем на порядок больше дрейфовой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.