Лавинно-стримерный переход. Структура стримера. Головка стримера. Катодонаправленный и анодонаправленный стримеры при импульсном воздействии напряжения, страница 7

                                                                  (1)

 В заданный момент времени концентрация электронов в лавине распределена по Гауссовому закону, в цилиндрических координатах концентрацию можно записать так:   

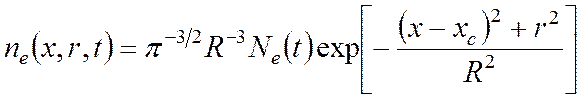                                                                                        (22)

Здесь R – характерный радиус лавины, расстояние от центра, на котором концентрация спадает в e раз. Он растет со временем по закону:

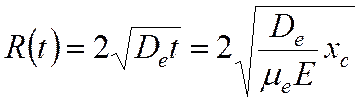                                                (33)

Ионы распределены по широкой области пространства, и мы пренебрежем влиянием их поля.

Напряженность поля складывается из напряженности внешнего поля E₀ и напряженности собственного поля лавины E'. Плотность заряда в лавине распределена сферически симметрично относительно центра. Благодаря сферической симметрии распределения заряда, мы сможем найти выражение для напряженности электрического поля лавины.

Зафиксируем момент времени и введем сферические координаты с радиальной координатой η. Связь с цилиндрическими координатами x,r:

                                               

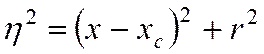
Согласно (22), плотность заряда в сферических координатах:

                                    

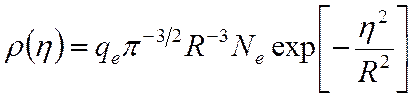
Здесь q_e – заряд электрона, N_e – полное число электронов в лавине.

Напряженность собственного электрического поля будет, очевидно зависеть лишь от радиальной координаты η. Для того, чтобы найти собственное электрическое поле лавины, воспользуемся теоремой Гаусса – выберем сферу S с радиусом r0 и центром, совпадающим с центром лавины. Тогда справедливо:

                                               

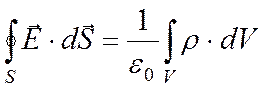
Или, переходя к сферическим координатам:

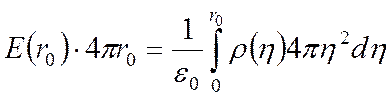                                            (44)

Интеграл в (44) можно взять с использованием специальной функции:

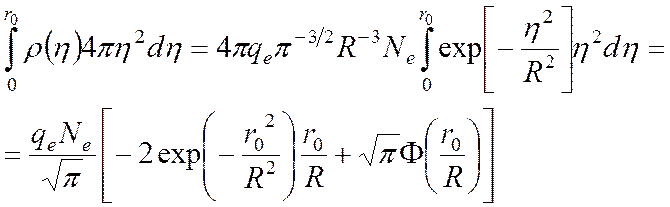                                                                            (5)

Специальная функция Ф(x) есть интеграл от функции Гаусса:

                                            

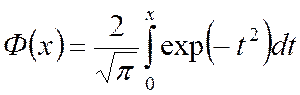
Подставляя результат (5) в (44), мы получаем напряженность поля в зависимости от радиальной координаты r₀:

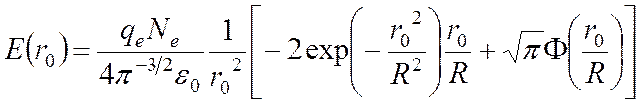
Графики зависимости плотности заряда и напряженности поля от радиальной координаты в фиксированный момент времени приведены на рисунке 117.

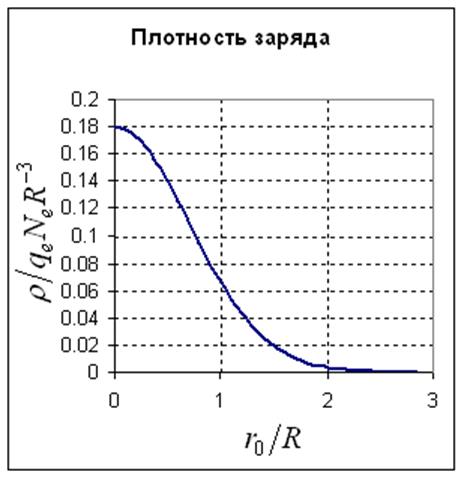
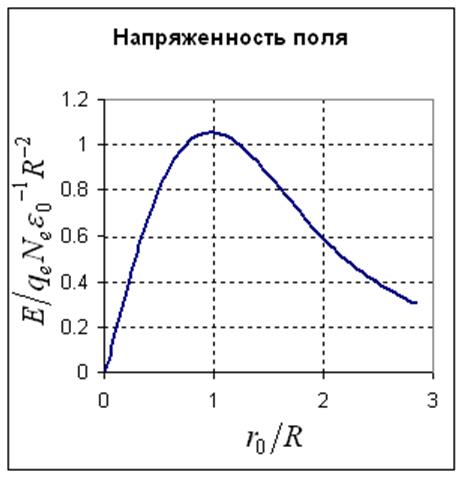
Рисунок 117. Плотность заряда и напряженность поля в лавине в фиксированный момент времени в зависимости от радиальной координаты. Величины приведены к безразмерному виду.

Напряженность поля распределена неоднородно – она нулевая в центре лавины и падает на далеких расстояниях. Максимальная напряженность достигается на расстоянии R от центра лавины – на расстоянии, где концентрация электронов в e раз меньше, чем в центре лавины. Максимальная напряженность поля равна:

                                                 

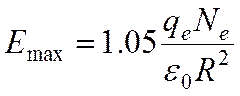
Для оценки можно отбросить множитель 1,05 и принять значение E_max за характерное значения напряженности собственного поля в лавине E_л – помня, что это максимальное значение напряженности поля в лавине.

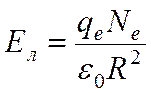                                                                                (6)

Учтем теперь зависимость параметров в (6) от времени. Число электронов в лавине и радиус растут по мере продвижения. Пусть x_c – центр лавины. Учитывая выражения (1) и (33), мы получаем зависимость напряженности собственного поля лавины E_л от координаты центра лавины x_c:

                                        

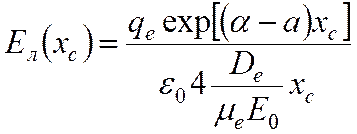
Лавинно-стримерный переход происходит, когда напряженность собственного поля лавины E_л становится сравнима с напряженностью внешнего поля E₀. То есть можно записать уравнение, которое позволит приблизительно определить момент перехода:

                                            

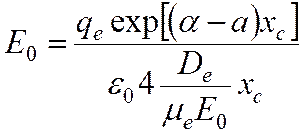
И здесь сразу заметно, что E₀ в правой и левой части сокращаются. Это значит, что координата центра лавинно-стримерного перехода не будет зависеть от напряженности поля: