Если мы имеем дело с лавиной в однородном поле эта малая доля электронов не играет особой роли – частота ионизации для нее равна частоте ионизации в основной части лавины. Однако в данной задаче ситуация иная – малая «опережающая» доля лавины попадает в область с высокой напряженностью поля, где частота ионизации гораздо больше, чем там, где остался центр лавины.
Попробуем математически описать ситуацию. Будем считать, что центр лавины покоится на месте, опережающий поток электронов распространяется гораздо быстрее центра. Будем работать с относительными единицами, пусть в центре лавины величина потока равна 1. Падение потока вследствие упругих ударов описывается функцией Гаусса:
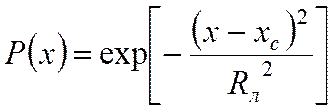
Рост потока вследствие ионизации можно описать, используя коэффициент ионизации α:
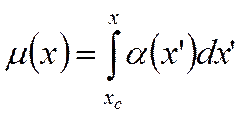
Результат действия обоих факторов можно описать произведением коэффициентов P и µ. Получаем коэффициент усиления γ:
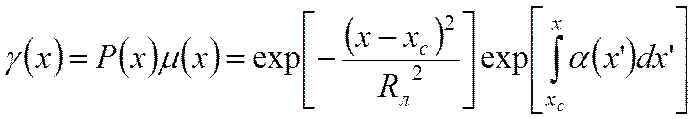
Этот коэффициент позволяет оценить влияние опережающего потока. Если он гораздо меньше единицы, важными являются только процессы в центре лавины, процессы на периферии не играют роли. Если он много больше единицы, напротив, электроны на периферии могут благодаря высокой частоте ионизации создать концентрации больше, чем в центре лавины.
График на рисунке 5 показывает зависимость коэффициента усиления от координаты для нескольких положений центра лавины. Если лавина находится далеко от сферы, (кривая xc=0.4 мм), опережающий поток не оказывает влияния на ситуацию – коэффициент усиления падает у электрода до очень низких (около 10-2) значений. При расстоянии центра лавины от сферы 0,35 мм ситуация промежуточная – ионизация позволяет коэффициенту усиления оставаться порядка единицы. А уже при расстоянии от сферы 0,3 мм коэффициент усиления позволяет увеличить концентрацию электронов у электрода примерно в 8 раз по сравнению с концентрацией в центре лавины.
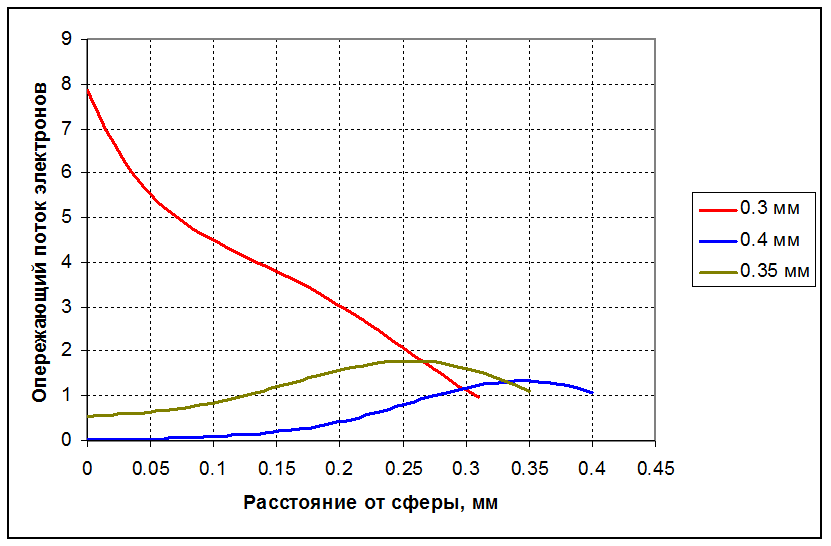
Рисунок 5. Коэффициент усиления опережающего потока электронов. Разные кривые приведены для разных положений центра лавины. Система сфера-сфера, радиус сферы 1 мм, напряжение 9 кВ, азот. Электроны движутся справа налево.
Разумеется, величины, введенные выше, определены не совсем корректно, однако эти оценки позволяют сравнить два фактора – малость числа электронов на периферии лавины и быстро растущий коэффициент ионизации. Полный расчет динамики электронов по силам, в конечном счете, лишь программным пакетам. Из сделанных выше оценок ясно, по крайней мере, что кажущийся странным результат – возникновение нового максимума «далеко» от лавины – не противоречит физическим соображениям, более того, такой результат можно было ожидать.
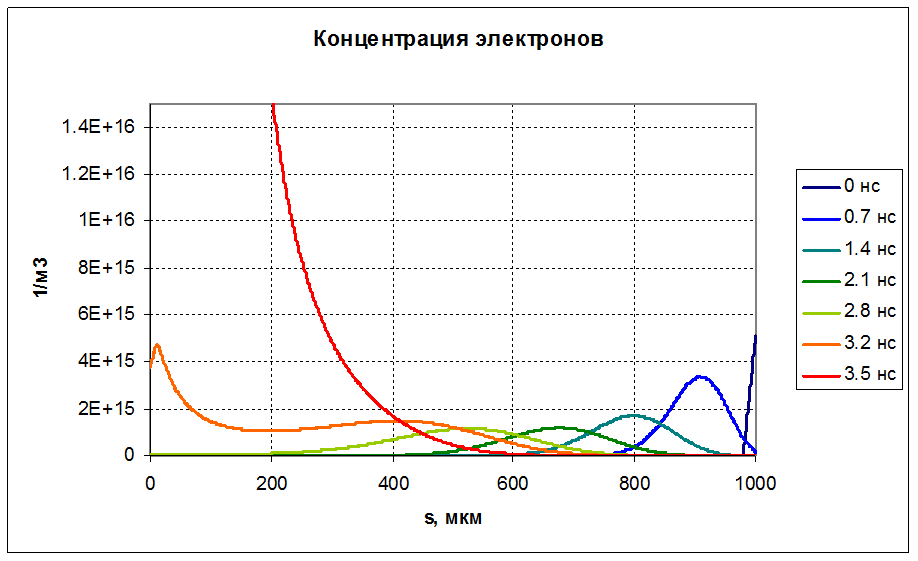
Рисунок 6. Начальный этап развития лавины. Переход от максимума в центре лавины к максимуму у электрода.
В результате действия опережающих электронов значительная концентрация электронов у сферы возникает, когда центр лавины находится еще далеко от электрода. Это значит, что еще значительное время область у поверхности будет «впитывать» электроны, приходящие из основной части лавины. Причем по мере приближения центра лавины к поверхности, приходящих электронов будет все больше. На этом этапе растет концентрация электронов у поверхности электрода.
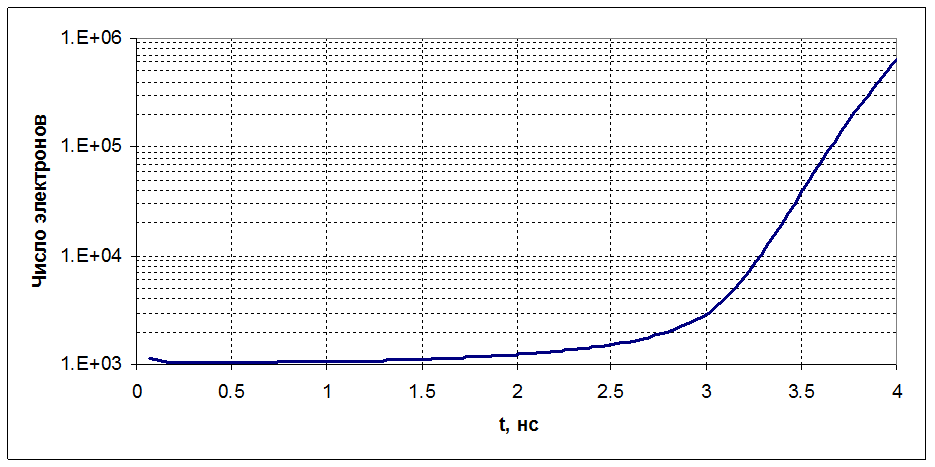
Рисунок 7. Полное число электронов в системе в зависимости от времени.
На рисунке 7 показано полное число электронов в системе в зависимости от времени. До 2 нс о лавинном процессе говорить не приходится. За это время число электронов возрастает всего на 20% по сравнению с начальным. Между тем центр лавины проходит за это время 300 мкм, то есть 30% длины системы. Затем рост активизируется, к 3 нс число электронов успевает возрасти в 3 раза по сравнению с начальным. Но как раз около 3 нс происходит смена максимума – из центра лавины он перемещается к поверхности электрода.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.