Кондуктометрия. Теоретическая интерпретация электропроводности электролитов. Учет сил взаимодействия. Аномалии электропроводности, страница 5

Для концентрированных растворов пользуются эмпирическими формулами. Одной из лучших следует признать формулу Шидловского

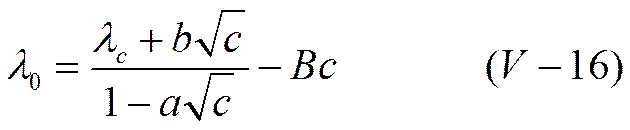
где В — некоторый эмпирический коэффициент. Первый член пра­вой части уравнения (V-16) отвечает формуле Онзагера (V-13), кото­рую можно написать как

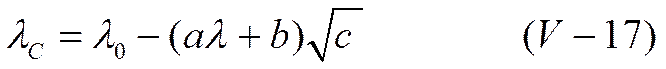
или

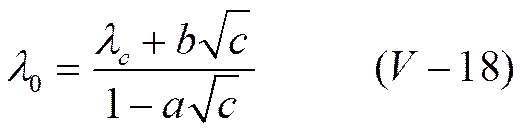
Эффект Вина и дисперсия электропроводности

Вин (1928) нашел, что при кратковременных импульсах тока электропроводность раствора растет с напряженностью поля. Вна­чале она увеличивается медленно, затем, при больших полях, быстрее и, наконец, при еще более высоких полях достигает неко­торого предела. Независимо от концентрации раствора, для каждого данного электролита этот предел отвечает его электропровод­ности при нулевой концентрации. В случае слабых электролитов Вин обнаружил еще более явно выраженный рост электропровод­ности с увеличением напряжения, установив, что чем меньше степень диссоциации электролита, тем заметнее увеличивается его электропроводности, стремясь к электропроводности при нулевой концентрации,

Результаты, полученные Вином, казались вначале совершенно невероятными. Они противоречили общепринятому представлению о приложимости закона Ома к растворам электролитов. Действи­тельно, по закону Ома

сопротивление R (или обратная ему величина электропроводности) для данной системы является неизменной величиной и, следователь­но, напряженность поля должна зависеть линейно от силы тока. Из опытов же Вина следовало, что при высоких значениях Δψ величина сопротивления R перестает быть постоянной и начинает падать с напряженностью поля. Следовательно, напряженность поля увеличивается непропорционально силе тока, и закон Ома в этом случае уже не оправдывается. Были высказаны предполо­жения, согласно которым эффект Вина является результатом каких-то неучтенных, вторичных явлений. Предполагалось, например, что падение сопротивления при высоких полях связано с разогре­вом электролита. Однако и расчеты, и дополнительные исследо­вания, поставленные по усовершенствованной методике с исполь­зованием кратковременных импульсов тока (при которых повышение температуры исключалось), подтвердили сделанное Вином наблю­дение о влиянии напряженности поля на электропроводность электролитов.

Применительно к сильным электролитам эффект Вина можно объяснить на основе теории электропроводности Дебая —Онзагера. Согласно представлениям Дебая и Гюккеля, в растворе каждый ион окружен ионной атмосферой с радиусом l/χ. Пока скорость его движения мала (по сравнению со скоростью разрушения и образо­вания ионной атмосферы), тормозящие эффекты, связанные с ион­ной атмосферой, сохраняются, и величина электропроводности при данной концентрации равна

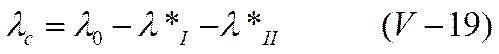
Однако, как известно, скорость ионов при увеличении напря­женности поля не остается постоянной, а растет в соответствии с уравнением (IV-10)

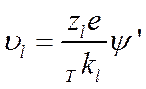
При достаточно высоком значении ψ' может оказаться, что путь, пройденный ионом за время разрушения старой и образования новой ионной атмосферы, т. е. за удвоенное время релаксации τ_r, будет равен или больше радиуса ионной атмосферы

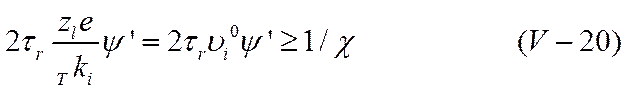
В этих условиях ион выйдет за пределы ионной атмосферы. Ионная атмосфера не будет успевать образовываться в каждом новом месте нахождения иона и, следовательно, ее суммарный тормозящий эффект уменьшится. При помощи уравнения (V-20) можно прибли­женно оценить ту напряженность поля, при которой начнет про­являться эффект Вина. Используя уравнение (V-10)

для времени релаксации и подставляя его в выражение (V-20), получим для искомой напряженности поля

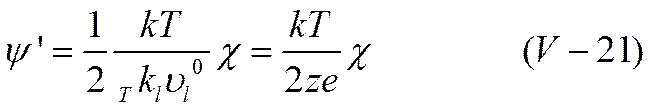
В случае 1-1 валентного электролита при комнатной температуре уравнение (V-11) упрощается до

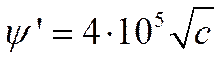
Таким образом для 0,001 н. раствора 1-1 валентного электролита эффект Вина начнет проявляться при полях порядка 10⁴, а для 1 н. — при 4-10⁵ в/см.

Дальнейшее повышение напряженности поля приведет к такой скорости движения ионов, при которой ионная атмосфера вообще не будет успевать образовываться. Исчезнут все связанные с ней тормозящие эффекты. Не будет наблюдаться изменения электро­проводности ни за счет электрофоретического эффекта, ни за счет релаксационного. В этом случае