Кондуктометрия. Теоретическая интерпретация электропроводности электролитов. Учет сил взаимодействия. Аномалии электропроводности, страница 4

Другой тормозящий эффект также связан с существованием ионной атмосферы и ее влиянием на движение ионов. Было установлено, что образование и разрушение ионной атмосферы протекает с большой, но с конечной скоростью. Характеристикой этой скорости служит так называемое время релаксации τ_r, которое можно рассматривать как величину, обратную константе скорости созда­ния или разрушения ионной атмосферы.

Время релаксации зависит от ионной силы раствора, его вязкости и диэлектрической постоянной и выражается уравнением

где _Tk — коэффициент внутреннего трения раствора; k — константа Больцмана; Т — абсолютная температура и χ — характеристическая длина по теории Дебая и Гюккеля. Для водного раствора 1-1 валентного электролита уравнение (V-10) упрощается и время релаксации можно приближенно рассчитать по уравнению

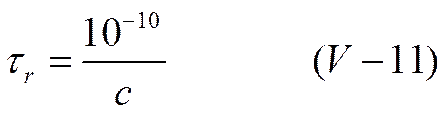
где с — концентрация электролита.

При перемещении центрального иона проходит какое-то время, пока старая ионная атмосфера разрушится и возникнет новая. Поэтому позади иона будет всегда находиться некоторый избыток заряда противоположного знака, и возникающие электрические силы притяжения будут тормозить его движение. Этот эффект торможения называется релаксационным. Если изменение эквива­лентной электропроводности, связанное с релаксационным эффек­том, обозначить через λ _II , то уменьшение электропроводности при переходе от нулевой концентрации (идеальный раствор) к концен­трации с дается уравнением

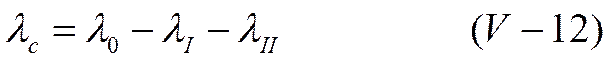
в котором учитываются и электрофоретический, и релаксационный эффекты.

Дебай и Гюккель вывели теоретические формулы для λ _I  и λ _II , в которые входит одна эмпирическая константа. Их расчеты были улучшены в дальнейшем Онзагером. Последний принял во внима­ние то обстоятельство, что движение ионов не совершается по пря­мой, а ионная атмосфера представляет собой статистическое обра­зование. Уравнение Онзагера имеет следующий вид:

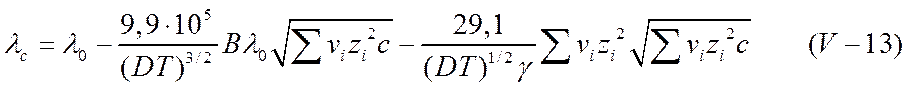
где

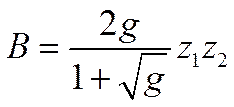
a

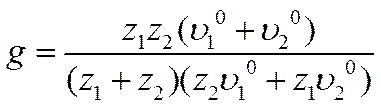
и γ - вязкость растворителя.

Для водных растворов 1-1 валентных электролитов при 25° С уравнение (IV-13) принимает вид

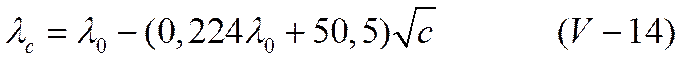
Уравнения (IV-13) и (IV-14) совпадают по виду с эмпирическим законом квадратного корня Кольрауша (Закон кубического корня, применимый в области умеренных концен­траций, не вытекает из теории Онзагера, но его можно получить как след­ствие теории Гхоша). Они позволяют теорети­чески предсказать численное значение константы А уравнения Кольрауша.

Формула Онзагера согласуется с опытными данными в той обла­сти концентраций, где приложим закон квадратного корня. При увеличении концентрации сходимость с опытом ухудшается. Урав­нение Онзагера следует рассматривать как эквивалент первого приближения теории Дебая и Гюккеля применительно к явлениям электропроводности. Оно дает поэтому лишь предельное ее значе­ние при концентрации электролита, приближающейся к нулю, т. е. касательную к кривой зависимости электропроводности от концен­трации. Подобно тому, как это было сделано во втором приближе­нии теории Дебая и Гюккеля при рассмотрении равновесия в раство­рах электролитов, можно было бы попытаться учесть влияние конечных размеров ионов и ввести параметр α в уравнения для электропроводности. Такие попытки были сделаны Канеко (1932), Фалькенгагеном (1952), Онзагером и Фуоссом (1955) и др. Питc (1953), следуя Ла Меру, учел, кроме того, дополнительные члены разложения в ряд показательной функции (см. стр. 53), а Робинсон и Стоке (1955) —изменение вязкости раствора с концентрацией. Введение среднего диаметра ионов а, являющегося эмпиричес­кой константой, и использование экспериментального значения вязкости позволили получить лучшую сходимость с опытом и рас­пространить видоизмененное таким образом уравнение Онзагера на электропроводность более концентрированных растворов. Одна­ко уравнения, полученные при этом, настолько сложны, что прак­тическая их ценность становится иллюзорной. Так, например, в уравнении Онзагера и Фуосса

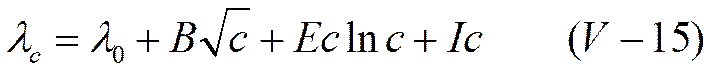
появляется логарифмический член и наряду с константой Е, кото­рая определяется теми же параметрами, что и константа В перво­начального уравнения Онзагера, входит величина I, зависящая от размера ионов.