В этих соотношениях:
d – диаметр голого проводника, м;
dиз – диаметр изолированного проводника, м;
dпр – толщина изоляционной прокладки, м.
Эквивалентный коэффициент теплопроводности равен:
- в обмотках с рядовой укладкой проводников
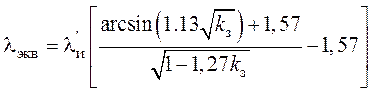 , (4,7)
, (4,7)
- в обмотках с шахматной укладкой проводников
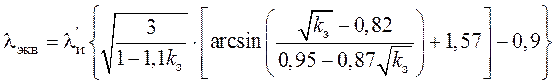 . (4,8)
. (4,8)
Эквивалентный коэффициент
теплопроводности промежутков между проводниками ![]() рассчитывается
по (4,5), а расчетное значение воздушных промежутков
рассчитывается
по (4,5), а расчетное значение воздушных промежутков ![]() определяется
по соотношениям:
определяется
по соотношениям:
- при рядовой укладке - 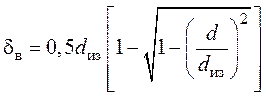 ,
,
- при шахматной укладке - 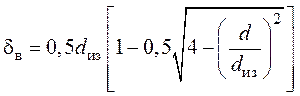 .
.
Для всыпных обмоток из круглых проводников, укладываемых в полузакрытый паз аналитический расчет эквивалентного коэффициента теплопроводности невозможен, так как неопределенными являются промежутки между проводниками вследствие многократного перекрещивания проводников. В [5, 6] на основании значительного экспериментального материала аппроксимирована зависимость для определения эквивалентного коэффициента теплопроводности таких обмоток.
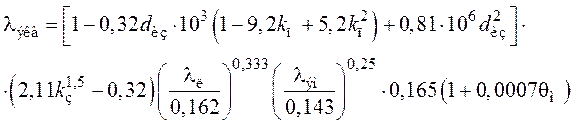 ,
(4,9)
,
(4,9)
где:
![]() - коэффициент теплопроводности
пропиточного состава,
- коэффициент теплопроводности
пропиточного состава, 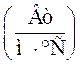 ;
;
![]() - коэффициент теплопроводности
изоляции провода,
- коэффициент теплопроводности
изоляции провода, 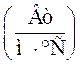 ;
;
![]() - коэффициент заполнения паза
медью;
- коэффициент заполнения паза
медью;
![]() - коэффициент пропитки;
- коэффициент пропитки;
![]() - допустимая температура для выбранного
класса изоляции,
- допустимая температура для выбранного
класса изоляции, ![]() .
.
Формула (4,9) выведена для обмоток из проводников с эмалевой изоляцией. Однако, она пригодна для расчета эквивалентного коэффициента теплопроводности обмоток из проводников с волокнистой изоляцией (ПСД, ПСДК и т.д.). В этом случае по рекомендациям [3] вместо коэффициента 0,165 берется 0,2.
4.3.2. Определение коэффициентов теплоотдачи
Нагрев отдельных частей электрической машины в значительной степени определяется условиями теплообмена между поверхностью активных частей и охлаждающей средой.
По данным [6] в электрических машинах с воздушным охлаждением конвективные тепловые сопротивления обуславливают от 50 до 80% нагрева обмоток. Решение задачи о конвективном теплообмене базируется на математическом описании процесса конвекции и его условий. Однако, опыт показывает, что расчет коэффициентов теплоотдачи на основе классических зависимостей а большинстве случаев не даёт достаточно достоверных результатов ввиду сложности учета большого количества факторов, определяющих условия теплоотдачи на границе раздела сред.
В связи с этим важное значение в решении задач конвективного теплообмена играют экспериментальные методы, позволяющие определить коэффициенты теплоотдачи по результатам обработки данных исследований как на моделях, так и на натурных образцах. Научная основа эксперимента базируется на теории теплового подобия [3, 4, 5, 6].
На основе теории теплового подобия протекающие процессы теплообмена описываются по результатам эксперимента в виде критериального уравнения с использованием безразмерных критериев, что позволяет распространить результаты ограниченного числа экспериментов на максимально возможное число реальных устройств. Чаще всего при исследовании тепловых процессов в электрических машинах применяются критерии подобия, краткая характеристика которых приводится ниже.
Критерий Рейнольдса 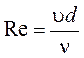 характеризует характер движения среды
(ламинарный или турбулентный) и представляет собой отношение инерционных сил
движущейся среды к силам внутреннего трения.
характеризует характер движения среды
(ламинарный или турбулентный) и представляет собой отношение инерционных сил
движущейся среды к силам внутреннего трения.
Критерий Нуссельта 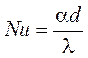 представляет собой безразмерную форму коэффициента
теплоотдачи и связывает между собой коэффициент теплоотдачи с поверхности с
теплопроводностью охлаждающей среды.
представляет собой безразмерную форму коэффициента
теплоотдачи и связывает между собой коэффициент теплоотдачи с поверхности с
теплопроводностью охлаждающей среды.
Критерий Прандтля 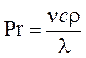 является сложной физической константой
охлаждающей среды и определяет её свойства.
является сложной физической константой
охлаждающей среды и определяет её свойства.
Критерий Фурье 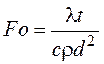 определяет
соотношение между темпом изменения окружающих условий и темпом перестройки
температурного поля внутри тела.
определяет
соотношение между темпом изменения окружающих условий и темпом перестройки
температурного поля внутри тела.
Критерий Био 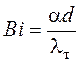 характеризует
меру отношения температурного перепада в теле к температурному перепаду между
телом и охлаждающей средой.
характеризует
меру отношения температурного перепада в теле к температурному перепаду между
телом и охлаждающей средой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.