Тепловые расчеты электрических машин. Поле температуры. Процессы передачи тепла. Дифференциальное уравнение теплопроводности. Понятие тепловых сопротивлений, страница 2

Как правило _, причем обычно _. Однако в ряде случаев, при определении перегревов необходимо использовать это соотношение (таким образом определяется перегрев поверхности корпуса закрытых электрических машин без искусственного обдува, работающих в спокойной окружающей воздушной среде).

В большинстве случаев при практических расчетах без ущерба для их точности можно принять , тогда получаем:

.

Здесь  называется результирующим  (или полным) коэффициентом теплоотдачи. Так как , то при естественном охлаждении необходимо учитывать передачу тепла как излучением, так и конвекцией. При искусственной конвекции с достаточно большими скоростями движения охлаждающей среды относительно нагретой поверхности коэффициент  и передачей тепла за счет излучения можно пренебречь. В этом случае .

4.2. Дифференциальное уравнение теплопроводности. Понятие тепловых сопротивлений.

Тепловые процессы в телах описываются дифференциальным уравнением теплопроводности для нестационарного трехмерного поля с распределенными по объему внутренними источниками тепла [3,4], которое устанавливает связь между изменениями температуры в пространстве и во времени и описывает процессы переноса тепла внутри тела.

,

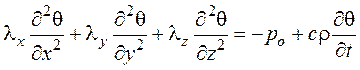где: p_o – удельные потери в единице объема (объемная плотность тепловыделении), ;

       с – теплоемкость, .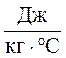

Аналитическое решение этого уравнения в общем виде не реализуемо. Однако, на практике приходится решать конкретные задачи, позволяющие упростить уравнение теплопроводности и получить аналитические решения [3, 4, 5, 6]. Так в электрических машинах в подавляющем большинстве случаев требуется рассчитать тепловое состояние в установившемся режиме 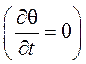, а реальное трехмерное поле можно без ущерба для точности расчета свести к одномерному. Такое поле характерно для теля, толщина которого много меньше ширины и высоты (). В случае наличия внутренних источников тепла поле в теле описывается уравнением Пуассона

,

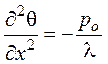а в случае отсутствия  - уравнением Лапласа

.

Эти уравнения решаются простым интегрированием, а общие решения имеют вид:

-  при наличии внутренних источников тепла :

,

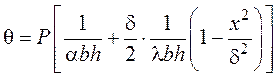-  при отсутствии внутренних источников тепла :

.

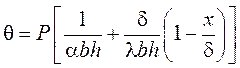В этих соотношениях: P – тепловой поток (полные потери в теле), Вт.

При тепловых расчетах электрических машин требуется рассчитать как максимальную температуру, так и среднюю. Максимальное значение температуры тела с внутренними источниками тепла соответствует значению x=0.

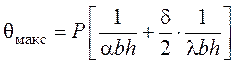
Средняя температура равна:

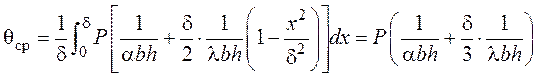
Для тела охлаждаемого с одной стороны без внутренних источников тепла (потери сосредоточены на неохлаждаемой стороне) максимальная температура равна (x=0):

.

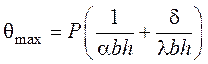Анализ полученных соотношений позволяет сделать вывод, что тело с внутренними источниками тепла может быть заменено телом без них с эквивалентным преобразованием размеров. В общем виде соотношение для расчета температуры запишется в виде:

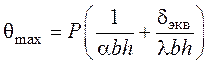
Для тел без источников тепла , для тел с внутренними источниками тепла при расчете максимальных температур 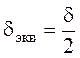, а средних .

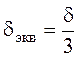По аналогии с электрическими цепями ( - аналог напряжения, Р – аналог тока) выражение в круглых скобках представляет собой тепловое сопротивление,

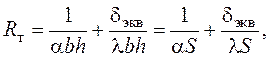
где: S – поверхность через которую передается тепло, м².

Тепловое сопротивление имеет две составляющие:

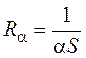 - тепловое сопротивление конвекции, ;

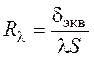 - тепловое сопротивление теплопроводности ( термическое сопротивление), .

Таким образом, температура тела описывается соотношением , которое положено в основу теплового расчета электрических машин по методу эквивалентных тепловых схем.

4.3 Определение коэффициентов теплопроводности и теплоотдачи при тепловых расчетах электрических машин

4.3.1 Коэффициент теплопроводности

композиционных структур.