Обоснование финансовых и инвестиционных решений в условиях риска, страница 3

·  β = 0, акции предприятия не реагируют на изменения рынка и не ограничиваются никакими рисками (гос. облигации)

·  β<1, ценные бумаги на предприятии менее рискованные, чем в целом по рынку

·  β>1, ценные бумаги предприятия более рискованные, чем в целом по рынку (их доходность зависит от колебаний рынка)

·  увеличение β коэффициента в динамике на предприятии свидетельствует о том, что инвестиции в эти ценные бумаги становятся более рискованными

·  снижение β коэффициента в динамике на предприятии свидетельствует о том, что инвестиции в эти ценные бумаги становятся менее рискованными

При подборе акций в оптимальный пакет используют следующие критерии:

·  в пакет включают акции, если их β коэффициент >1. причем они должны приносить доход больший, чем в среднем по рынку (Nj>r)

·  колебание акций, включенных в пакет, должно происходить таким образом, чтобы показатель тесноты связи вариации (корреляции) норм доходности был отрицательным (риск портфеля снижается вследствие его диверсификации) ф-ла 5.25 на стр.358

Американский экономист Джек Трейнор разработал интегральный критерий, который учитывает риск. Для определения риска , связанного с колебанием рынка он разработал прямую, назвав ее ХАРАКТЕРИСТИЧЕСКОЙ ЛИНИЕЙ, которая показывает соотношение между доходностью по анализируемому портфелю и доходностью рынка. Наклон этой прямой определяет относительную изменчивость доходов портфеля относительно доходов совокупного рынка. Для формирования прямой он предложил безрисковые ценные бумаги, которые можно объединять с любыми портфелями.   Для расчета наклона линии портфеля рынка или коэффициента портфеля он предлагает использовать следующую формулу:

, где

Nr- доходность ценных бумаг в среднем на рынке

Nf- доходность безрисковых ценных бумаг

βr- β-коэффициент рынка

Наклон для прямой ценных бумаг рассчитывается по формуле:

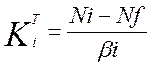
Ni – доходность i-го вида ценных бумаг (портфеля)

βi- β-коэффициент i-го вида ценных бумаг (портфеля)

Чем больше уклон линии (относительно значения ), тем лучше состав портфеля для всех инвесторов, независимо от отношения к риску. Эффективным может считаться портфель, для которого значение находится выше линии рынка.

Аналогично графику линии рынка Дж.Трейнора можно построить график линии капитала рынка В. Шарпа. По оси координат откладывается среднеквадратическое отклонение, при чем линия капитала рынка пройдет через точки (0; N_f) и (σ_r ;N_r). Критерий В.Шарпа в отличие от коэффициента портфеля Дж.Трейнора учитывает диверсифицированность портфеля инвестиций (то есть систематический и несистематический риск). Эти два критерия дополняют один другой.

Модель САРМ, разработанная В.Шарпом предусматривает определение необходимой нормы доходности по акциям конкретного предприятия, которые покрывают риски и имеет вид:

N_н = Nf + (Nr – Nf)

N_н – необходимая доходность акций предприятия

Nr- доходность ценных бумаг в среднем на рынке

Nf- доходность безрисковых ценных бумаг

Разница (Nr – Nf) имеет видимую интерпретацию – это рыночная (то есть средняя) премия за риск вложенного инвестором капитала не в государственные безрисковые облигации, а в обычные акции предприятий, имеющие определенный риск. Аналогично разницу (Nн  – Nf) рассматривают как премию за риск на вложения капитала в ценные бумаги конкретного предприятия.

Важной характеристикой САРМа является линейность относительно степени риска, то есть β-коэффициент аортфеля определяется как средневзвешенное β-коэффициента акций:

β _порт. = 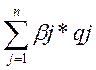, где

βj – значение β-коэффициента j-го актива в портфеле

β _порт. - значение β-коэффициента портфеля

n – количество различных активов в портфеле

q_j – часть j-го актива в портфеле