Теорія поля. Властивості векторних полів. Електромагнітне поле. Нестаціонарні поля. Системи Максвела для електромагнітного поля

Лекція 13

Теорія поля

План:

 13.1. Властивості векторних полів.

 13.2. Електромагнітне поле.

 13.3. Основні операції векторного аналізу

           в циліндричній та сферичній системах координат         

 13.4. Нестаціонарні поля. Системи Максвела для електромагнітного поля.

 13.5. Запитсння для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Математичні факти з попередніх розділів, які використовуються в даній лекції.

Пригадайте матеріал з розділів: векторн алгебра – скалярний і векторний добуток, проекція вектора на вісь; кратні інтеграли – циліндрична та сферична системи координат; криволінійні та поверхневі інтеграли – інтегрування повного диференціала, формула Остроградського – Гауса;

13.1. Властивості векторних полів

Серед різноманітних векторних полів найбільший інтерес (із-за практичних властивостей) викликають векторні поля, для яких  або , або ж дорівнюють нулю і дивергенція і ротор. Розглянемо такі поля докладніше.

I. П о т е н ц і а л ь н е     п о л е. З такими полями ми зтикалися при при вивченні криволінійних інтегралів, а також в курсі фізики. Від потенціального поля пішла назва функції, яка характеризує це поле. Векторне поле  називається потенціальним, якщо існує функція  така, що .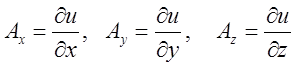

Функція – називається потенціальною функцією векторного поля або просто потенціалом. Згідно з визначенням . І тоді . Але ж, як ми довели в попередній лекції, що завжди . Тому критерієм потенціальності поля є рівність нулю його ротора в усіх точках.Таким чином, у всіх точках потенціального поля ротор дорівнює нулю. Тому потенціальне поле швидкостей течії рідини часто називають безвихровим, у такому полі рідина не утворює вирів. 

У потенціальному полі циркуляція по будь-якому замкнутому контур дорівнює нулю.               Робота в силовому потенціальному полі, як ми це знаємо з розгляду криволінійних інтегралів,  дорівнює різниці потенціалів у кінцевій  і початковій точках:

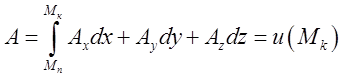
                                                          (13.1)

Вивчення потенційного поля значно полегшується тим, що це поле цілком визначається заданням однієї скалярної функції його потенціалу. Проекції вектора поля  будуть при цьому частинними похідними цієї функції за відповідними координатами.  Довільне ж векторне поле задається трьома скалярними функціями — проекціями вектора  на осі координат.

Якщо векторне поле  займає поверхнево-однозв’язну  область і у всіх його точках , то поле потенціальне. 

 Це, майже автоматично, випливає з того, що при  обов’язково і .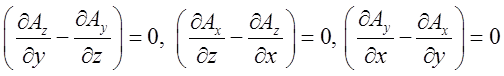

А це значить, що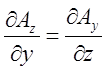; ; 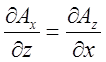 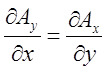і, згідно теореми з лекції 8,  існує функція повний диференціал якої дорівнює  ;

це рівносильно тому, що тобто, що  є потенціалом поля.

В лекції 8 для відновлення скалярної потенціальної функції  за відомими координатами її градієнту, ми використали криволінійний інтеграл і одержали таку формулу:=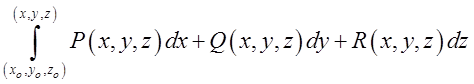

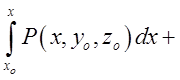
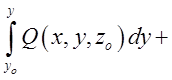
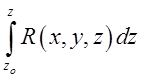=. Але в тому випадку, коли область існування поля має центр на початку координат, а який завгодно промінь, з початком в О(0,0,0), перетинає її границю лише один раз (нехай це буде навіть на нескінченності), то потенціал векторного поля можна знайти за формулою:

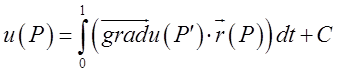,                                                                         (13.2)

де С – постійна; – радіус-вектор точки; точка при  пробігає відрізок ОР прямої, яка проходить через точки О і Р. Цю формулу ми подаємо без доведення, яке можна знайти в глибоких курсах теорії поля.

П.1.  Знайти потенціал поля .

Розв. Областю визначення поля є весь тривимірний простір. Всі промені, які виходять з точки О(0,0,0), перетинають границю області лише один раз – на нескінченності. Для знаходження потенціалу маємо право застосувати формулу (13.2). Обчислимо скалярний добуток, який стоїть під інтегралом  . Підставимо це в формулу (13.2).

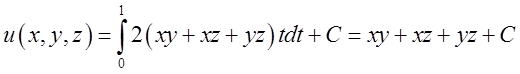. Легко переконатись, що  дасть той вектор, що був нам заданий за умовою. Відповідь:.

II. Т р у б ч а с т е  (с о л е н о їд а л ь н е)  п о л е. Векторне поле ,  у всіх точках якого дивергенція дорівнює нулю:, називається трубчастим або соленоїдальным.

Щоб охарактеризувати властивості такого поля, уведемо визначення просторово- однозв'язної області.

Тривимірна область  називається просторово-однозв'язною, якщо разом з будь-якою простою замкнутою поверхнею їй належить і область, обмежена цією поверхнею.

Просторово однозв'язними областями є куля, еліпсоїд, куб, тор, півпростір і т.п.