Нехай тепер поле
створене системою електричних зарядів ![]() .
Позначимо через
.
Позначимо через ![]() напруженість поля,
створюваного зарядом
напруженість поля,
створюваного зарядом ![]() , а через
, а через ![]() – результуючу напруженість. Тоді
– результуючу напруженість. Тоді 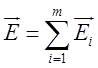 .
.
Проекція вектора ![]() на
напрямок нормалі
на
напрямок нормалі ![]() до будь-якої поверхні дорівнює
до будь-якої поверхні дорівнює
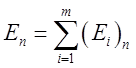 , а тому потік через
поверхню буде
, а тому потік через
поверхню буде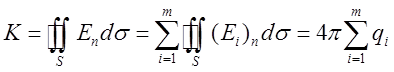 , де
, де 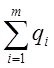 – сума зарядів,
які лежать усередині розглянутої поверхні.
– сума зарядів,
які лежать усередині розглянутої поверхні.
Ця формула відіграє важливу роль у вивченні електричних полів і називається вона електростатичною теоремою Гауса.
II. М а г н і т н е п о л е п р я м о л і н і й н о г о с т р у м у.
В лекції 11 (приклад 6) ми знайшли рівняння
векторних ліній нескінченно довгого прямолінійного провідника з струмом силою
І. В лекції 12, з точністю до постійного коефіцієнта ![]() ,
який залежить від одиниць вимірювання, ми обчислили проекції вектора
,
який залежить від одиниць вимірювання, ми обчислили проекції вектора ![]() напруженості магнітного поля на вісі
координат
напруженості магнітного поля на вісі
координат 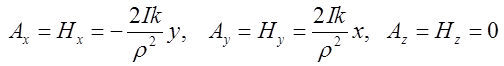 .
.
Обчислимо дивергенцію цього поля 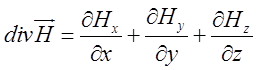 .
. 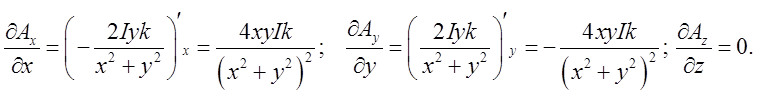 При
підстановці одержимо
При
підстановці одержимо ![]() . В лекції 12 ми з’ясували, що
ротор цього поля також дорівнює 0, тобто воно всюди, за винятком точок на вісі
провідника, є безвихрове.
. В лекції 12 ми з’ясували, що
ротор цього поля також дорівнює 0, тобто воно всюди, за винятком точок на вісі
провідника, є безвихрове.
Отже, циркуляція поля по будь-якому контурі, що не оточує вісь Оz (вісь провідника), дорівнює нулю. Якщо ж контур оточує вісь Оz, то такого висновку зробити не можна, тому, що будь-яка поверхня, натягнута на такий контур, перетинає вісь Оz, а в точках цієї вісі поле не визначене.
Обчислимо
циркуляцію по колу радіуса R,
що лежить у площині Оху, з центром на початку
координат: ![]()
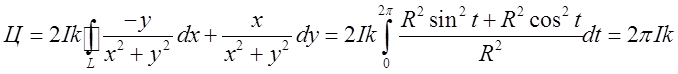 .
.
Як бачимо з результату, величина циркуляції не залежить від радіуса кола, більше того можно довести, що вона залишається однією і тією ж для будь-якого контуру, який обходить вісь Оz.
13.3. Основні операції векторного аналізу
в циліндричній та сферичній системах координат
Оскільки інженерна механіка пов’язана з
механізмами, в яких переважають круглі тіла і такі, що обертаються (циліндри,
поршні, вали, підшипники, шківи, шестерні і т. п. ), то при наукових
дослідженнях зручніше, а інколи просто необхідно, користуватися криволінійними
просторовими системами координат. Найпоширенішими є дві розглянуті нами системи
при вивченні потрійних інтегралів: циліндрична і сферична. І хоч ці системи
координат, як і звична прямокутна, також ортогональні (в кожній точці простору
три її координати перпендикулярні між собою), але в криволінійних координат є
докорінна відмінність від прямокутної, а саме: в декартовій системі вектори
базису постійні для всіх точок простору і дорівнюють відповідно ![]() ; в криволінійних системах вони змінюють
свій напрямок при переході від однієї точки до іншої. Ми в лекції 5 бачили, що
при переході з прямокутної системи в циліндричну чи сферичну елемент об’єму
; в криволінійних системах вони змінюють
свій напрямок при переході від однієї точки до іншої. Ми в лекції 5 бачили, що
при переході з прямокутної системи в циліндричну чи сферичну елемент об’єму ![]() . У кожному випадку з’являються множники,
які назвали якобіанами переходу.
. У кожному випадку з’являються множники,
які назвали якобіанами переходу.
Аналогічна картина буде і при
переході від прямокутної системи координат до криволінійних систем координат
для операцій векторного аналізу. Не вдаючись в подробиці обчислення, так
званих, коефіцієнтів Ламе, приведемо вирази для градієнта, дивергенції і ротора
в циліндричній і сферичній системах координат. Нижче: ![]() –
орти базису циліндричної системи координат;
–
орти базису циліндричної системи координат; ![]() – орти
сферичної системи координат, причому тут кут
– орти
сферичної системи координат, причому тут кут ![]() – це
кут між віссю Oz і r (а ми в лекції 5
брали цей кут між площиною хОу і r). Функції
– це
кут між віссю Oz і r (а ми в лекції 5
брали цей кут між площиною хОу і r). Функції ![]() задані у відповідній системі
координат.
задані у відповідній системі
координат.
Оператори теорії поля в циліндричних координатах:
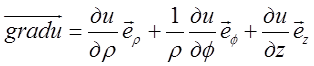 . (13.5)
. (13.5)
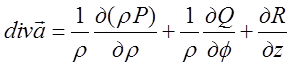 . (13.6)
. (13.6)
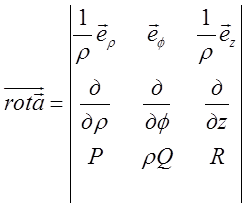 . (13.7)
. (13.7)
.Оператори теорії поля в сферичних координатах:
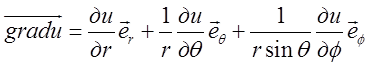 . (13.8)
. (13.8)
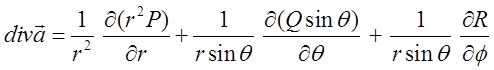 . (13.9)
. (13.9)
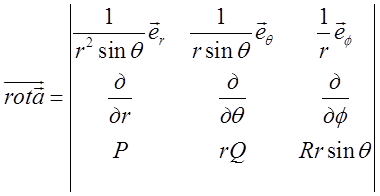 . (13.10)
. (13.10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.