Теорія поля. Властивості векторних полів. Електромагнітне поле. Нестаціонарні поля. Системи Максвела для електромагнітного поля, страница 3

Розв. Наше поле визначене у всьому тривимірному просторі. Промінь, який вийде з початку координат перетне границю області лише в одній точці, яка знаходиться на нескінченності, а тому маємо право застосувати вище приведену формулу (13.3) для знаходження векторного потенціалу. В точці  маємо .

Обчислимо підінтегральний вираз, тобто векторний добуток .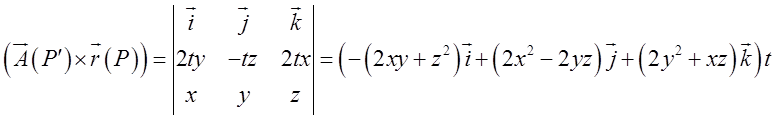

Підставимо знайдене значення в (13.3) і проінтегруємо.

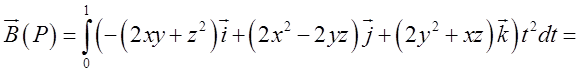
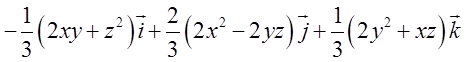=. Як згадувалось вище, поле знаходиться неоднозначно, тобто ми знайшли одне з полів. Легко переконатися, що .

 III. Г а р м о н і ч н е   п о л е. Векторне поле, що являється  одночасно і потенціальним і трубчастим, називається  гармонічним. Оскільки поле потенціальне, його можна записати  у вигляді , де и –  потенціал поля. Умова трубчастості поля означає, що . Цей факт ми довели в попередній лекції. Там же ми переконалися, що 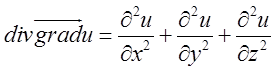  і ввели оператор Лапласа 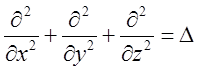. Таким чином з

Функції , що підкоряються цій умові, називаються гармонічними або Лапласовими. Вони відіграють важливу роль у різних розділах теоретичної фізики.

10.2. Електромагнітне поле.

 Поряд з силовим векторним полем тяжіння, полем швидкостей рухомого тіла, одним з найважливіших в нашому житті  є  електромагнітне поле. Розглянемо кілька простих прикладів.

I. Е л е к т р и ч н е    п о л е. Нехай  – поле напруженості точкового заряду q, розміщеного в початку координат.  Тоді вектор напруженості, який ми одержали в лекції 9 (задача 9.2), матиме вид: 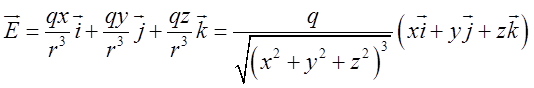. Векторними лініями такого поля служать промені, що виходять з початку координат, тобто з заряду.

Поле напруженості  є полем потенціальним. В лекції 9 ми знайшли потенціал  поля  . Він є 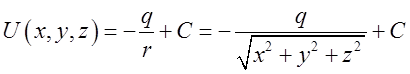. При С=0    .

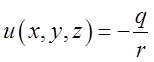 В фізиці домовились за потенціал поля брати функцію 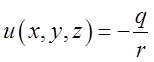, взяту з протилежним знаком, тобто 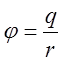. Тому  .

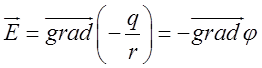Таким чином, різниця потенціалів між двома точками поля дорівнює взятій з протилежним знаком роботі, виконаній силами поля при переміщенні одиничного позитивного заряду з першої точки в другу. Знайдемо дивергенцію поля напруженості. Обчислимо відповідні похідні.

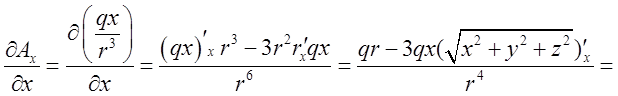
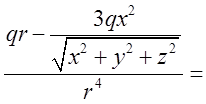
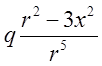. Аналогічно:  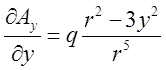,  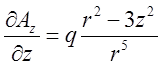    . Підставимо в формулу для дивергенції.

.

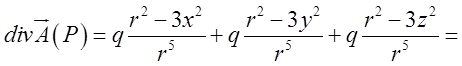
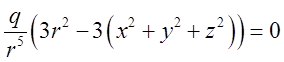Отже,

Потік вектора  через будь-яку замкнуту поверхню, що не містить усередині себе початку координат, дорівнює нулю.

Якщо ж початок координат, тобто заряд, міститься усередині поверхні, то такого висновку зробити вже не можна, тому, що на початку координат поле не визначене.

Обчислимо потік вектора Е через сферу, радіуса R з центром на початку координат. На  поверхні цієї сфери напрямок вектора  збігається з напрямком нормалі, тобто радіуса-вектора.  Тому 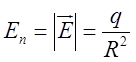  . Звідси потік  дорівнює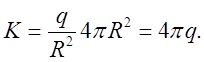

Ми бачимо, що величина потоку не залежить від радіуса сфери R. Легко показати, що величина потоку залишається незмінної для будь-якої замкнутої поверхні, що оточує початок координат.

Візьмемо таку довільну поверхн. і помістимо вcередину неї яку-небудь сферу з центром на початку координат (рис. 13.2). Розіб'ємо тепер тіло, обмежене поверхнею на декілька  конусів з вершиною на початку координат. Кожен такий, конус має вигляд зображений на рис. 13.3. Тому що частина конуса, розміщена між ділянкою сфери і даною поверхнею, є векторної трубкою,  а дивергенція поля дорівнює нулю то потоки

                                                            

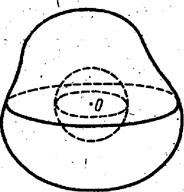
Рис. 13.2.                                                                          Рис.13.3.

через ділянки сфери і поверхні рівні між собою. Складаючи потоки через усі такі ділянки поверхні, ми й одержуємо, що потік вектора  через будь-яку поверхню, що оточує початок координат  дорівнює потоку через сферу, тобто . Будемо вважати, що внутрішня сфера має радіус, який дорівнює одиниці. Тоді потік через ділянку поверхні  буде дорівнює , де  – площа поверхні  сфери одиничного радіуса, в яку проектується ділянка поверхні. Величину  –  називають тілесним кутом, під яким поверхню   видно з початку координат.