Теорія поля. Властивості векторних полів. Електромагнітне поле. Нестаціонарні поля. Системи Максвела для електромагнітного поля, страница 2

Порожня куля, очевидно, не є просторово однозв'язною областю. Узагалі, якщо в тілі існують внутрішні порожнини (хоча б у вигляді окремих точок), то однозв’язності у вище розглянутому сенсі не буде. Наприклад, якщо при виготовлені металевого зливку  утворилися внутрішні раковини (порожнечі), то зливок буде займати просторово неоднозв’язну область.

Повернемося до вивчення трубчастого поля.

Якщо трубчасте поле займає просторово однозв'язну область, то потік вектора через будь-яку замкнуту поверхню, розташовану в цьому  полі, дорівнює нулю;

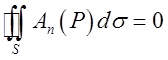                                                                                           (13.2)

Це є прямий  наслідок теореми Остроградського – Гауса : .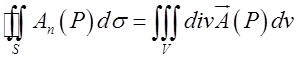

Якщо трубчасте поле займає область, що має внутрішні порожнечі (найчастіше у виді окремих

особливих точок), то потік вектора через замкнуті поверхні, які обмежують ці точки, може і не дорівнювати нулю (там може бути джерело або стік векторного поля).

Пояснимо зміст назви «трубчасте поле», вважаючи, що воно займає просторово-однозв'язну область. Візьмемо в цьому полі яку-небудь площадку  і проведемо через кожну

               Рис. 13.1                   точку її границі векторні лінії. Ці лінії обмежують частину простору, названу векторною трубкою (рис13.1). Рідина при своїй течії увесь час рухається по такій трубці, не перетинаючи її стінок. Розглянемо частину такої трубки, обмежену площадкою  і яким-небудь перетином  (рис.13.1). Потік вектора через поверхню, що обмежує цю частину трубки, дорівнює нулю. Отже,

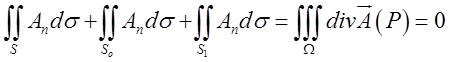, де S – бічна поверхня трубки, а  – її зовнішня нормаль. Так як на бічній поверхні трубки нормалі   перпендикулярні, до векторів поля, то 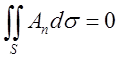. Звідси випливає, що    .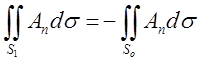

Змінивши напрямок нормалі на площадці ,тобто узявши внутрішню нормаль , одержимо 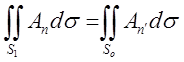   Це означає, що потік вектора в напрямку векторних ліній через кожен перетин векторної трубки один і той же, тобто в полі  без джерел  і стоків через кожен перетин векторної трубки протікає одна і  та ж  сама  кількість рідини. Згідно з розглянутими в лекції 12 властивостями векторних диференційних операцій другого порядку , тобто поле ротора будь-якого векторного поля – трубчате.

Справедливо і зворотнє тверження. Таким чином критерієм соленоїдальності векторного поля є рівність нулю його дивергенції.

Кожне трубчасте поле є полем ротора деякого векторного поля, тобто якщо , то існує таке векторне поле , що.

Вектор  називають вектором-потенціалом даного поля. Так як  , то . Ми бачимо, що поле  визначається неоднозначно, а з точність до градієнта деякого скалярного поля. Це випливає з розв’язку системи скалярних диференціальних рівнянь, яка одержується з векторного рівняння .

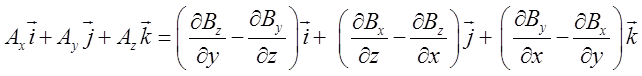Система має вид: ;    ;      .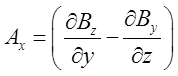

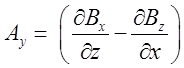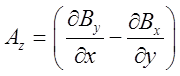Знаходити вектор–потенціал з цієї системи дуже складно, а тому без доведення ми приведемо формулу, за якою при деяких умовах легко знайти вектор-потенціал. Такою умовою  для області V трубчатого векторного поля  є те,  що кожен промінь, який виходить з початку координат О(0,0,0) повинен перетинати границю області V лише в одній точці. При цій умові вектор-потенціал можна знайти за формулою:

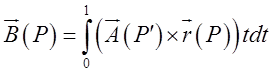,                                                                                    (13.4)

де  – радіус-вектор точки , а точка  під час зміни параметра t від 0 до 1 пробігає відрізок ОР.

Зверніть увагу на спорідненість і відмінність формул (13.2) і (13.4). При знаходженні скалярного потенціалу підінтегральна функція є скалярним добутком – це в (13.2), а  при знаходженні векторного потенціалу підінтегральна функція є векторним добутком – це в (13.4). За винятком множника t, на який домножують векторний добуток в (13.4) все інше в них збігається.  

П.2. Знайти векторний потенціал соленоїдального поля .