Математика \ Дифференциальные уравнения

Теоремы Штурма. Краевые задачи

Страницы работы

11 страниц (Word-файл)

Скачать файл

Содержание работы

ЛЕКЦИЯ № 12.

Тема: ТЕОРЕМЫ ШТУРМА. КРАЕВЫЕ ЗАДАЧИ

ПЛАН

12.1 Теоремы Штурма

12.2 Понятие о краевых задачах

12.3 Задача Штурма-Лиувилля. Понятие о собственных числах и собственных функциях

12.4 Решение краевых задач методом функции Грина

12.1 Теоремы Штурма

Возьмем уравнение

(12.40)

и рассмотрим два его линейно независимые решения и . Мы видим, что между двумя последовательными корнями решения находится один, и только один, корень решения . И это не случайно. Любые линейно независимые решения любого линейного уравнения 2-го порядка, имеющего колебательные решения, обладает этим свойством.

Т е о р е м а Ш т у р м а. Нули двух действительных линейно независимых решений однородного линейного уравнения 2-го порядка с действительными коэффициентами взаимно отделяются.

Пусть имеем однородное линейное уравнение 2-го порядка

, (12.41)

линейно независимые решения которого обозначим через и . Полагаем . Предположим, что обращается в ноль не менее двух раз на , а и являются его двумя последовательными нулями в этом промежутке:

Докажем, что тогда существует одно, и только одно значение , , для которого . Т.к. функции и линейно независимые, то и , ибо в противном случае

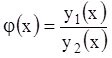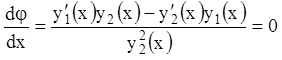обращался бы в ноль в этих точках. Положим, что совсем не имеет корней на и рассмотрим функцию . Она непрерывна на , имеет непрерывную производную и обращается в ноль на концах отрезка. Поэтому по теореме Ролля ее производная должна обращаться в ноль хотя бы один раз в интервале , т.е. в т. , , а это невозможно, т.к. числитель этой дроби является определителем. В поисках линейно независимых решений, т.е. при предположение о том, что совсем не имеет корней на неверно, и функция имеет хотя бы один корень на промежутке . Их не может быть два, потому что тогда между ними на основании только что доказанного находился бы ноль функции и, значит, и не были бы последовательными нулями этой функции, как это предполагалось.

Рассмотренная теорема теряет силу, если решения недействительные. Так, например, комплексное решение уравнения (12.40) не имеет совсем нулей на любом промежутке действительной переменной .

В ы в о д из теоремы: если одно решение линейного уравнения имеет на промежутке более двух нулей, то все решения этого уравнения являются колебательными.

Теорема сравнения.

Предыдущая теорема устанавливает, что решения одного и того же линейного уравнения имеют одинаковый характер (оба колебательные или неколебательные). Естественно поставить вопрос о сравнении решений двух различных уравнений.

Т е о р е м а. Пусть даны два линейные уравнения 2-го порядка, записанные в самосопряженной форме:

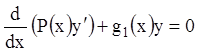и (12.42)

, (12.43)

где на . Если на , то решения уравнения (12.43) колеблются не медленнее, чем решения уравнения (12.42). Точнее: между двумя корнями решения (12.42) находится хотя бы один корень каждого решения уравнения (12.43).

Д о к а з а т е л ь с т в о. Пусть и решения уравнений (12.42) и (12.43) соответственно, т.е.

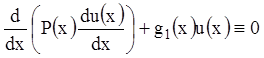, (12.44)

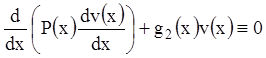, (12.45)

а и последовательные нули: и на .

Умножив (12.44)на , а (12.45) на и, вычитая почленно, получим:

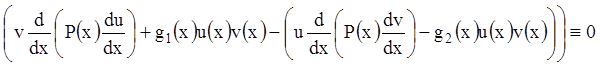
или

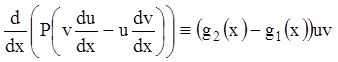. (12.46)

Интегрируя (12.46) в пределах от до , находим:

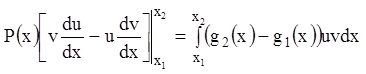. (12.47)

Положим теперь, что не имеет корней на , тогда на функция однозначна, например .

Не ограничивая общности положим, что и на . На основании наших допущений правая часть равенства (12.47) неотрицательна. Рассмотрим левую часть последнего равенства.

Она отрицательная, т.к. и по допущению, и , т.к. на и и . Равенства и исключаются, т.к. в этом случае . Значит, мы пришли к противоречию. Т.о., предположение, что не имеет корней на неверно, т.е. обращается в ноль не меньше одного раза на интервале . Теорема доказана.