![]() на
интервале
на
интервале ![]() .
.
Р е ш е н и е. Запишем его в
сопряженной форме, вычислив 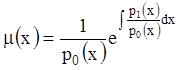 ;
; 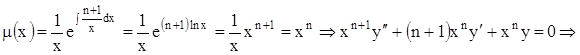
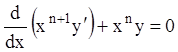
Пусть ![]() изменяется в промежутке
изменяется в промежутке ![]() . Сравним два уравнения:
. Сравним два уравнения:
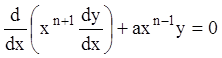 и
и 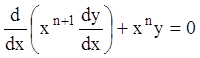 .
.
Здесь ![]() и
и
![]() , причем
, причем ![]() .
Первое из уравнений можно представить в виде:
.
Первое из уравнений можно представить в виде:
![]() или
или ![]() .
.
Это уравнение Эйлера. Частные решения ищем в виде:
![]() .
.
Подставляем в уравнения ![]() . Тогда получаем характеристическое
уравнение:
. Тогда получаем характеристическое
уравнение:
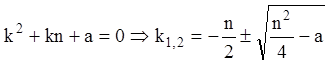 .
.
Положив 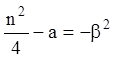 , получим
, получим 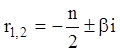 .
Общее решение
.
Общее решение
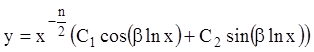 .
.
Если возьмем частное решение 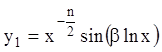 , то оно имеет бесконечное число нулей в
точках
, то оно имеет бесконечное число нулей в
точках 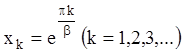 : тогда, в силу теоремы сравнения между
двумя последовательными нулями рассмотренного уравнения (при
: тогда, в силу теоремы сравнения между
двумя последовательными нулями рассмотренного уравнения (при ![]() ), будет находиться хотя бы один ноль
каждого решения уравнения:
), будет находиться хотя бы один ноль
каждого решения уравнения:
![]() . (12.48)
. (12.48)
О т в е т: каждое решение
уравнения (12.48) имеет бесконечное число корней на интервале ![]() .
.
Задачей Коши для
дифференциального уравнения называют задачу нахождения его частного решения,
удовлетворяющего заданным начальным условиям. Но при решении многих физических
задач (колебания струны, распространение тепла в стержне, диффузии веществ и
т.д.) найти решение дифференциального уравнения только на интервале ![]() и при этом должны выполнятся так называемые
краевые (граничные) условия, которые задаются не в одной точке (как в задаче
Коши), а на концах отрезка
и при этом должны выполнятся так называемые
краевые (граничные) условия, которые задаются не в одной точке (как в задаче
Коши), а на концах отрезка ![]() . Задача нахождения
решения дифференциального уравнения, удовлетворяющего заданным граничным
условиям, называется краевой задачей.
. Задача нахождения
решения дифференциального уравнения, удовлетворяющего заданным граничным
условиям, называется краевой задачей.
Рассмотрим постановку краевых задач для некоторых линейных дифференциальных уравнений второго порядка. Из теории линейных дифференциальных уравнений известно, что уравнение:
![]() , (12.49)
, (12.49)
где ![]() – непрерывные на
– непрерывные на ![]() функции,
имеет общее решение вида:
функции,
имеет общее решение вида:
![]() . (12.50)
. (12.50)
Функции ![]() и
и ![]() –
определенные на
–
определенные на ![]() и линейно независимые на этом
отрезке частные решения соответствующего однородного уравнения;
и линейно независимые на этом
отрезке частные решения соответствующего однородного уравнения; ![]() – любое частное решение неоднородного
уравнения (12.49);
– любое частное решение неоднородного
уравнения (12.49); ![]() – произвольные постоянные.
– произвольные постоянные.
Краевая задача для уравнения
(12.49) в общем случае формулируется так: найти на ![]() решения
этого уравнения, удовлетворяющие заданным граничным условиям. При этом
рассматриваются следующие граничные условия:
решения
этого уравнения, удовлетворяющие заданным граничным условиям. При этом
рассматриваются следующие граничные условия:
1) ![]() (условия первого типа).
(условия первого типа).
Геометрически это означает,
что требуется найти интегральную кривую дифференциального уравнения (26)
проходящую через данные точки ![]() и
и ![]() .
.
2) ![]() (условия второго типа).
(условия второго типа).
Геометрически это означает
отыскание интегральной кривой уравнения (12.49), которая бы пересекала прямые ![]() и
и ![]() под
заданными углами
под
заданными углами ![]() ,
, ![]() .
.
Эти условия могут быть представлены также в форме соответствующих линейных комбинаций:
![]() , (12.51)
, (12.51)
определяющих задачу со смешанными
граничными условиями, где ![]()
![]() – заданные числа; при этом в каждой из пар
– заданные числа; при этом в каждой из пар
![]() и
и ![]() ,
, ![]() и
и ![]() хотя бы
одно из чисел не равно нулю.
хотя бы
одно из чисел не равно нулю.
Например,
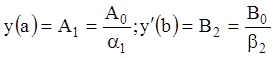 .
.
Геометрический смысл краевой
задачи с последними краевыми условиями: построить интегральную кривую уравнения
(12.49), которая проходила бы через точку ![]() и
пересекала бы прямую
и
пересекала бы прямую ![]() под углом
под углом ![]() .
.
3) ![]() – ограниченная величина при
– ограниченная величина при ![]() и
и ![]() (условия
третьего типа).
(условия
третьего типа).
Среди краевых задач существенное значение имеют однородные краевые задачи, с которыми связано, в частности, исследование собственных режимов движения различных физических систем.
Однородные краевые задачи – это задачи на отыскание решений однородных линейных дифференциальных уравнений при однородных граничных условиях.
Граничные условия называются
однородными, если из того факта, что функции (частные решения задачи) ![]() удовлетворяют этим условиям, следует, что
любая их линейная комбинация
удовлетворяют этим условиям, следует, что
любая их линейная комбинация 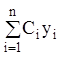 также удовлетворяет тем
же условиям.
также удовлетворяет тем
же условиям.
В частности, краевые условия
(12.51) будут однородными при ![]() . Очевидно, что таким
условиям удовлетворяет функция
. Очевидно, что таким
условиям удовлетворяет функция ![]() , которая в силу этого
является решением однородной краевой задачи. Однако, тривиальное решение редко
интересует исследователя и чаще всего ищут не- нулевые решения. Отметим, что
каждая однородная краевая задача может либо не иметь ненулевых решений вообще,
либо имеет их бесчисленное множество. Эта особенность краевых задач требует
такой их постановки, которая обеспечивает существование, а при необходимости и
единственность решения.
, которая в силу этого
является решением однородной краевой задачи. Однако, тривиальное решение редко
интересует исследователя и чаще всего ищут не- нулевые решения. Отметим, что
каждая однородная краевая задача может либо не иметь ненулевых решений вообще,
либо имеет их бесчисленное множество. Эта особенность краевых задач требует
такой их постановки, которая обеспечивает существование, а при необходимости и
единственность решения.
Рассмотрим пример, имеющий вполне определенный прикладной смысл.
П р и м е р 1: Найти решения дифференциального уравнения
![]() , (12.52)
, (12.52)
удовлетворяющие краевым условиям
![]() . (12.53)
. (12.53)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.