Отсюда следует, что задача о радиальных колебаниях мембраны приводит к задаче Штурма-Лиувилля, и ее решения можно представить в виде линейной комбинации (12.60) функций Бесселя нулевого порядка:
![]() .
.
Учитывая, что решение этой
задачи должно удовлетворять граничным условиям ![]() и
и ![]() ограничено при
ограничено при ![]() , надо в
силу второго условия принять
, надо в
силу второго условия принять ![]() (т.к.
(т.к. ![]() при
при ![]() ). Таким
образом, нами продемонстрирован один из вариантов применения функций Бесселя в
прикладных задачах.
). Таким
образом, нами продемонстрирован один из вариантов применения функций Бесселя в
прикладных задачах.
Рассмотрим краевую задачу для уравнения:
![]() (12.62)
(12.62)
с однородными граничными условиями
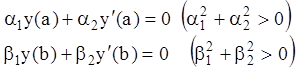 (12.63)
(12.63)
Будем предполагать, что рассматриваемая краевая задача имеет единственное решение.
Пусть ![]() -
какое-либо нетривиальное решение соответствующего однородного уравнения:
-
какое-либо нетривиальное решение соответствующего однородного уравнения:
![]() , (12.64)
, (12.64)
удовлетворяющее первому из граничных условий (12.63).
![]() ,
,
а ![]() -
нетривиальное решение уравнения (12.64), удовлетворяющее второму граничному
условию
-
нетривиальное решение уравнения (12.64), удовлетворяющее второму граничному
условию
![]() .
.
Тогда ![]() не
удовлетворяет второму граничному условию, так как в противном случае при любой
постоянной
не
удовлетворяет второму граничному условию, так как в противном случае при любой
постоянной ![]() функции
функции ![]() были бы
решениями краевой задачи (12.63)-(12.64) и наша исходная краевая задача
(12.62)-(12.63) имела бы бесконечное множество решений. Аналогично
доказывается, что
были бы
решениями краевой задачи (12.63)-(12.64) и наша исходная краевая задача
(12.62)-(12.63) имела бы бесконечное множество решений. Аналогично
доказывается, что ![]() не удовлетворяет первому граничному
условию. Итак:
не удовлетворяет первому граничному
условию. Итак:
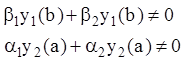 (12.65)
(12.65)
Построенные решения ![]() линейно независимы, так как в противном
случае они были бы пропорциональны и поэтому удовлетворяли бы одним и тем же
граничным условиям, что невозможно. Тогда общее решение (12.64) имеет вид
линейно независимы, так как в противном
случае они были бы пропорциональны и поэтому удовлетворяли бы одним и тем же
граничным условиям, что невозможно. Тогда общее решение (12.64) имеет вид ![]() , где
, где ![]() - произвольные
постоянные.
- произвольные
постоянные.
Решение неоднородного
уравнения (12.62) будем искать методом вариации произвольных постоянных.
Записывая решение ![]() в виде:
в виде:
![]() (12.66)
(12.66)
для нахождения функций ![]() и
и ![]() строим
систему линейных алгебраических уравнений:
строим
систему линейных алгебраических уравнений:
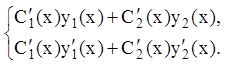
Решая эту систему, находим
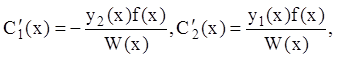 (12.67)
(12.67)
где 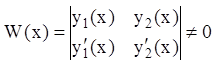 ,
как определитель Вронского, составленный для линейно независимых решений
,
как определитель Вронского, составленный для линейно независимых решений ![]() и
и ![]() .
Интегрируя (12.67), получаем:
.
Интегрируя (12.67), получаем:
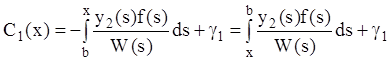 ,
,
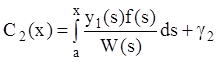 ,
,
где ![]() -
постоянные.
-
постоянные.
Подставляя найденные
выражения для ![]() и
и ![]() в
(12.66), получаем общее решение уравнения (12.62):
в
(12.66), получаем общее решение уравнения (12.62):
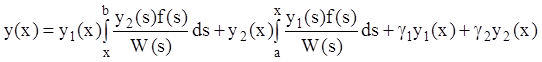 .
(12.68)
.
(12.68)
Дифференцируя (12.68) по ![]() , имеем
, имеем
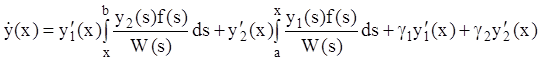 ,
(12.69)
,
(12.69)
так
как результаты дифференцирования интегралов равны 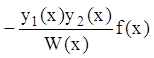 и
и 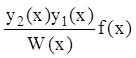 и сокращаются.
и сокращаются.
Потребуем теперь, чтобы
решение (12.68) удовлетворяло граничным условиям (12.63). Подставляя выражения
(12.68), (12.69) в первое из граничных условий (12.63), получим (так как ![]() ):
):
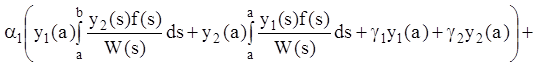
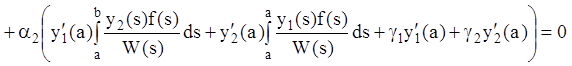 .
.
Группируя подобные члены, получаем
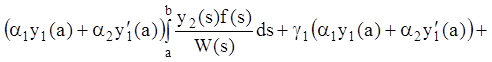
![]() .
.
Так как в силу первого
граничного условия (12.63) содержимое первых двух скобок равно нулю, а
последняя скобка в силу второго условия (12.65) не равна нулю, то последнее
равенство возможно лишь при ![]() .
.
Аналогично, используя второе
граничное условие, показывается, что ![]() . Тогда решение краевой
задачи (12.62)-(12.63) можно представить в виде
. Тогда решение краевой
задачи (12.62)-(12.63) можно представить в виде
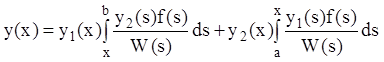
или:
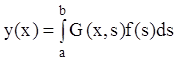 , (12.70)
, (12.70)
где:
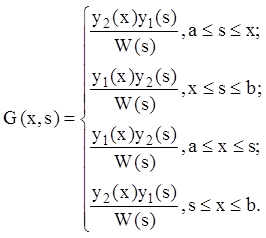 (12.71)
(12.71)
Построенная функция ![]() называется функцией Грина краевой задачи
(12.62)-(12.63). Таким образом, если функция Грина найдена, то решение краевой
задачи (12.62)-(12.63) задается формулой (12.70). Сама функция Грина от
называется функцией Грина краевой задачи
(12.62)-(12.63). Таким образом, если функция Грина найдена, то решение краевой
задачи (12.62)-(12.63) задается формулой (12.70). Сама функция Грина от ![]() не зависит (она определяется решениями
не зависит (она определяется решениями ![]() и
и ![]() однородного
уравнения (12.64)).
однородного
уравнения (12.64)).
Легко проверить, что функция
Грина ![]() при любом фиксированном
при любом фиксированном ![]() обладает следующими свойствами:
обладает следующими свойствами:
1) при
![]()
![]() удовлетворяет
однородному уравнению (12.64);
удовлетворяет
однородному уравнению (12.64);
2) при
![]() и
и ![]()
![]() удовлетворяет соответственно первому и
второму граничным условиям (12.52);
удовлетворяет соответственно первому и
второму граничным условиям (12.52);
3) при
![]()
![]() непрерывна;
непрерывна;
4) при
![]() производная
производная ![]() имеет
скачок равный 1:
имеет
скачок равный 1:
![]() .
.
Свойства 1) – 3) почти очевидны. Докажем свойство 4). В силу (12.71)
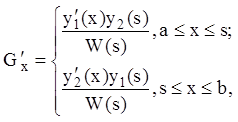
откуда следует, что:
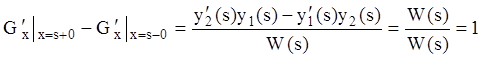 .
.
Можно показать, что свойства
1)- 4) однозначно характеризуют функцию Грина, то есть, что любая функция ![]() , обладающая свойствами 1)- 4), является
функцией Грина и имеет вид (12.71).
, обладающая свойствами 1)- 4), является
функцией Грина и имеет вид (12.71).
З а м е ч а н и е.
Использовать функции Грина особенно удобно в тех случаях, когда приходится
многократно решать краевую задачу (12.62)-(12.63) для различных правых частей ![]() .
.
П р и м е р. Построить функцию Грина для краевой задачи:
![]()
Решение: Общее решение соответствующего
однородного уравнения ![]() имеет вид
имеет вид ![]() , откуда находим
, откуда находим ![]() -
нетривиальное решение, удовлетворяющее первому граничному условию
-
нетривиальное решение, удовлетворяющее первому граничному условию ![]() (таких решений бесконечное множество).
Аналогично находим
(таких решений бесконечное множество).
Аналогично находим ![]() - нетривиальное решение, удовлетворяющее
второму граничному условию
- нетривиальное решение, удовлетворяющее
второму граничному условию ![]() . Тогда
. Тогда 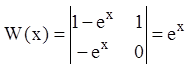 . Тогда по формуле (12.71) находим
. Тогда по формуле (12.71) находим
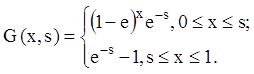
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.