К такому уравнению и краевым
условиям приводит, например, задача о колебаниях струны, зафиксированной в
неподвижных точках ![]() и
и ![]() .
Непосредственно видно, что
.
Непосредственно видно, что ![]() является решением
поставленной задачи, но это тривиальное решение. Дальше, говоря о решениях
краевой задачи, будем иметь в виду только нетривиальные решения. В
решаемой задаче возможны 3 случая.
является решением
поставленной задачи, но это тривиальное решение. Дальше, говоря о решениях
краевой задачи, будем иметь в виду только нетривиальные решения. В
решаемой задаче возможны 3 случая.
С л у ч а й I. ![]() (корни соответствующего
характеристического уравнения комплексные).
(корни соответствующего
характеристического уравнения комплексные).
![]() . Тогда
общее решение уравнения (12.52):
. Тогда
общее решение уравнения (12.52):
![]() .
.
Находим ![]() и
и ![]() ,
используя краевые условия (12.53):
,
используя краевые условия (12.53):
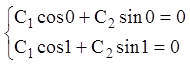 или
или 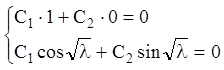
![]()
![]() и
и ![]() или
или ![]() . Если
. Если ![]() , то имеем тривиальное решение
, то имеем тривиальное решение ![]() . Если же
. Если же ![]() , то
, то ![]() или
или ![]() , тогда
решение запишется:
, тогда
решение запишется:
![]()
![]() .
.
С л у ч а й II. ![]() (корни действительные и кратные).
(корни действительные и кратные).
![]() . Тогда
общее решение запишется:
. Тогда
общее решение запишется:
![]() .
.
Используя краевые условия, получаем:
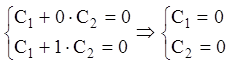 .
.
Решение тривиальное: ![]() .
.
С л у ч а й III. ![]() (корни действительные и разные).
(корни действительные и разные).
![]() . Общее
решение:
. Общее
решение:
![]() .
.
Учитывая граничные условия, получаем:
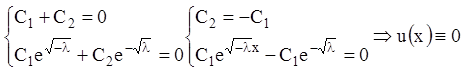 .
.
В ы в о д: если ![]() , то краевая задача (12.52)-(12.53) имеет
бесконечное число решений вида:
, то краевая задача (12.52)-(12.53) имеет
бесконечное число решений вида:
![]() .
.
Если же ![]() , то единственным решением будет
тривиальное решение
, то единственным решением будет
тривиальное решение ![]() .
.
Линейное дифференциальное уравнение вида
![]() (12.54)
(12.54)
называется уравнением Штурма-Лиувилля. (Штурм Ж. (1803-1855), Лиувилль Ж. (1809-1822) – французские математики).
К рассмотрению уравнений такого типа приводят решения физических задач о продольном изгибе стержня, о колебаниях ограниченной струны, круглой мембраны и некоторые другие.
Задачей Штурма-Лиувилля
называется краевая задача об отыскании на некотором отрезке ![]() ненулевых решений уравнения (12.54) из тех
значений
ненулевых решений уравнения (12.54) из тех
значений ![]() , при которых существуют такие решения,
удовлетворяющие одному из вариантов однородных краевых условий:
, при которых существуют такие решения,
удовлетворяющие одному из вариантов однородных краевых условий:
![]() ; (12.55)
; (12.55)
![]() ; (12.56)
; (12.56)
![]() ограничено
при
ограничено
при ![]() . (12.57)
. (12.57)
Условия (12.55) и (12.56) могут быть представлены по аналогии с равенствами (12.49) линейными комбинациями
![]() . (12.58)
. (12.58)
При решении задачи
предполагается, что в уравнении (12.54) функции ![]() ,
, ![]() непрерывны на
непрерывны на ![]() и,
кроме того,
и,
кроме того, ![]() ;
; ![]() –
некоторое число, параметр уравнения. Эти условия являются достаточными для
существования решения задачи Штурма-Лиувилля.
–
некоторое число, параметр уравнения. Эти условия являются достаточными для
существования решения задачи Штурма-Лиувилля.
Рассмотренный выше пример 1
является частным случаем задачи Штурма-Лиувилля при ![]() .
.
Значения ![]() параметра
параметра ![]() , при
которых существуют ненулевые решения уравнения (12.54), удовлетворяющие
однородным граничным условиям (12.58), называются собственными числами
(характеристическими значениями), а сами эти решения – собственными
функциями задачи Штурма-Лиувилля.
, при
которых существуют ненулевые решения уравнения (12.54), удовлетворяющие
однородным граничным условиям (12.58), называются собственными числами
(характеристическими значениями), а сами эти решения – собственными
функциями задачи Штурма-Лиувилля.
Множества всех собственных чисел и собственных функций задачи Штурма-Лиувилля обладают следующими основными свойствами:
1) все собственные числа неотрицательны;
2) количество собственных чисел бесконечно велико, но их можно перенумеровать в порядке возрастания, тогда они образуют некоторую монотонно возрастающую числовую последовательность;
3) каждому собственному числу соответствует собственная функция, определенная с точностью до некоторого постоянного множителя;
4) собственные
функции, соответствующие различным собственным числам, попарно ортогональны на ![]() с весом
с весом ![]() и образующим
бесконечную последовательность функций:
и образующим
бесконечную последовательность функций: ![]() .
.
Многие физические задачи приводят к уже известному нам уравнению Бесселя (12.31):
![]() . (12.59)
. (12.59)
Общее решение этого уравнения
при любом целом ![]() имеет вид:
имеет вид:
![]() , (12.60)
, (12.60)
где соответственно ![]() – функции Бесселя первого рода,
– функции Бесселя первого рода, ![]() – функции Бесселя второго рода (функции
Неймана) порядка
– функции Бесселя второго рода (функции
Неймана) порядка ![]() .
.
Так, при решении задачи о собственных
радиальных колебаниях круглой мембраны, закрепленной по контуру ![]() , приходят к уравнению:
, приходят к уравнению:
![]() ,
,
которое является частным случаем (при
![]() ) уравнения
) уравнения
![]() . (12.61)
. (12.61)
Покажем, что уравнение
(12.61) приводится с точностью до обозначений к уравнению (12.59), а с другой
стороны – к уравнению (12.54) Штурма-Лиувилля, т.е. что уравнения (12.61) и
(12.59) являются частными случаями уравнения (12.54). Выполним линейную замену
независимой переменной в уравнении (12.61), приняв ![]() (
(![]() ). При этом, перейдя от дифференцирования
по
). При этом, перейдя от дифференцирования
по ![]() к дифференцированию по
к дифференцированию по ![]() , найдем:
, найдем:
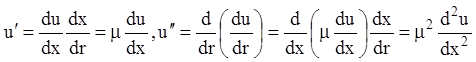 .
.
После подстановки ![]() и
и ![]() в
(12.61) имеем
в
(12.61) имеем
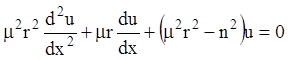
или
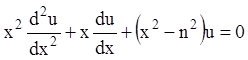 ,
,
т.е. уравнение Бесселя (12.59).
Умножив все члены уравнения
(12.61) на ![]() , получим
, получим
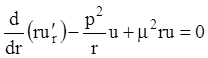 ,
,
т.е. уравнение Штурма-Лиувилля
(12.54), в котором 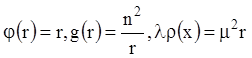 ,
, ![]() – параметр
уравнения, что и требовалось доказать.
– параметр
уравнения, что и требовалось доказать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.