Расчетная схема струйного насоса приведена на рисунке 17.
В отличие от газовых эжекторов, в струйных насосах необходимо учитывать гидравлические потери во всех элементах устройства - в рабочем сопле, во входном участке камеры смешения, в самой камере смешения и в диффузоре.
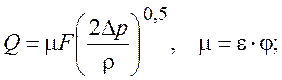
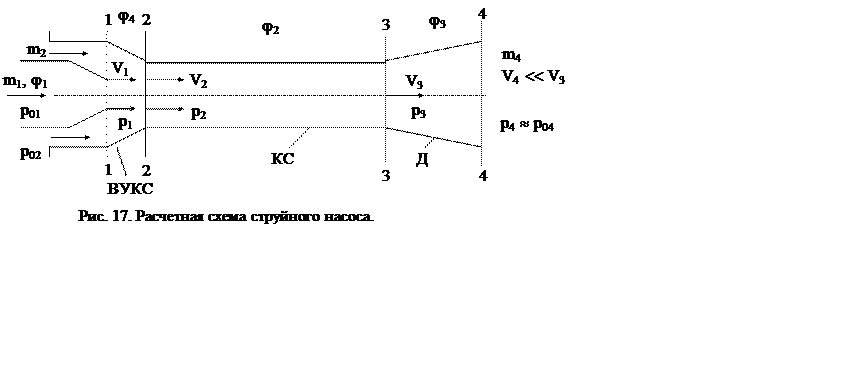 |
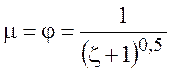 ,
,
![]() ,
,
![]() — коэффициент сужения струи. В нашем
случае e = 1.
— коэффициент сужения струи. В нашем
случае e = 1.
![]() — форма канала.
— форма канала.
ВУКС — входной участок камеры смешения;
КС — камера смешения;
Д — диффузор.
На ВУКС диаметр (площадь) рабочей струи ![]() не меняется. В каждом из рассмотренных
сечений:
не меняется. В каждом из рассмотренных
сечений: ![]() параметры потока постоянны по сечению.
Уравнение характеристик струйного насоса получим на основе уравнения импульсов
для камеры смешения. Количество движения (секундное) для потока проходящего
через входное сечение камеры смешения (КС):
параметры потока постоянны по сечению.
Уравнение характеристик струйного насоса получим на основе уравнения импульсов
для камеры смешения. Количество движения (секундное) для потока проходящего
через входное сечение камеры смешения (КС):
![]() (А)
(А)
Вычислим входящие в данное соотношение скорости:
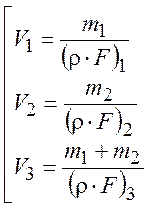
и давления
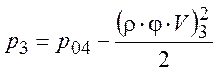
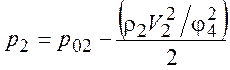
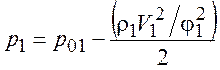 .
.
После подстановки в уравнение (А) и проведения тождественных преобразований, получим:
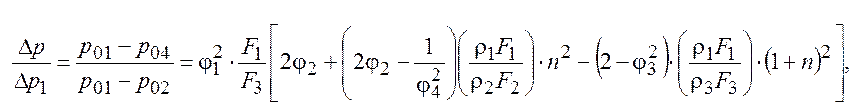 (1).
(1).
![]()
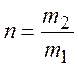 ;
; 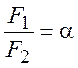 ;
; 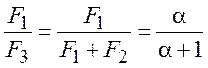 ;
;
Уравнение (1) с учетом принятых соотношений примет вид:
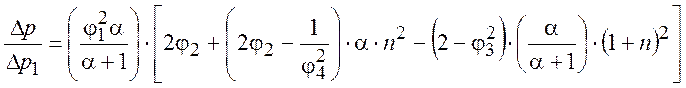 (2)
(2)
Из практики установлены следующие рекомендуемые значения коэффициентов скорости:
![]()
Подставив приведенные значения в уравнение (2), получим:
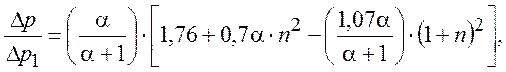 (2’)
(2’)
Следствия:
1.
Из выведенных уравнений (1), (2), (2’) можно
сделать вывод, что относительное повышение давления в струйном насосе
определяется геометрическим параметром ![]() и при
автомодельных режимах по числу Re (
и при
автомодельных режимах по числу Re (![]() не меняется с изменением
Re) струйные насосы различные по абсолютным размерам, но
с одинаковым относительным параметром
не меняется с изменением
Re) струйные насосы различные по абсолютным размерам, но
с одинаковым относительным параметром ![]() , дадут
одинаковое относительное повышение давления.
, дадут
одинаковое относительное повышение давления.
2.
Повышение давления в струйном насосе заданных геометрических размеров (правая
часть уравнения (1) равна константе) прямо пропорционально перепаду ![]() давлений в рабочем и эжектируемом соплах.
давлений в рабочем и эжектируемом соплах.
![]()
![]() — правая часть уравнения (1).
— правая часть уравнения (1).
Полученные уравнения справедливы для случая:

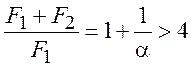
Такие СН называются низконапорными и находят
наибольшее распространение в практике. В высоконапорных СН: ![]() на начальном участке камеры смешения.
на начальном участке камеры смешения.
![]() за счет сжатия струи (
за счет сжатия струи (![]() —
площадь поперечного сечения струи) и расчеты по приведенным выше формулам дают
несколько завышенный результат. Максимальный относительный перепад давления
развивается струйным насосом при
—
площадь поперечного сечения струи) и расчеты по приведенным выше формулам дают
несколько завышенный результат. Максимальный относительный перепад давления
развивается струйным насосом при ![]() .
.

При рекомендуемых значениях ![]() ,
приведенных выше, и
,
приведенных выше, и 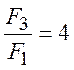 :
:
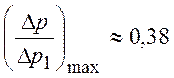 при
при 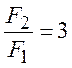 , т.е.
, т.е. 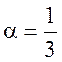
Для получения характеристики струйного насоса без
диффузора следует в уравнениях (1) или (2) положить ![]() .
.
Оценка эффективности работы СН осуществляется по его КПД:
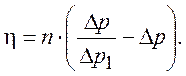
Лекция№7
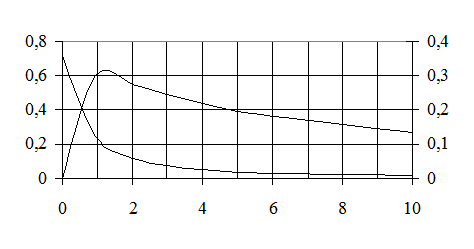
10. ДОСТИЖИМЫЕ ПАРАМЕТРЫ И ОПТИМАЛЬНОЕ a В СТРУЙНЫХ НАСОСАХ
Под достижимыми параметрами будем понимать
максимальное значение относительного перепада, ![]() .
Значения других параметров, при которых достигается максимальное значение
одного из перечисленных параметров, будем называть оптимальными.
.
Значения других параметров, при которых достигается максимальное значение
одного из перечисленных параметров, будем называть оптимальными.
При заданных ![]() и n
найдем соотношение площадей:
и n
найдем соотношение площадей:
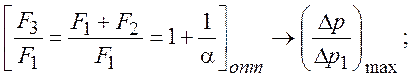
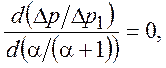 (*)
(*)
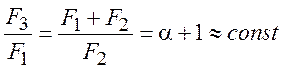
![]()
![]()
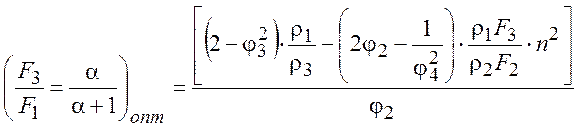 (4)
(4)
![]() заранее неизвестно, поэтому им в начале
задаются, вычисляют
заранее неизвестно, поэтому им в начале
задаются, вычисляют![]() , снова определяют
, снова определяют ![]() , уточняют его значения и опять производят
вычисления, пока не будет найдена связь, удовлетворяющая уравнению (4).
Подставим оптимальные значения площадей в уравнение характеристики СН, получим
выражение для максимального относительного повышения давления в СН.
, уточняют его значения и опять производят
вычисления, пока не будет найдена связь, удовлетворяющая уравнению (4).
Подставим оптимальные значения площадей в уравнение характеристики СН, получим
выражение для максимального относительного повышения давления в СН.
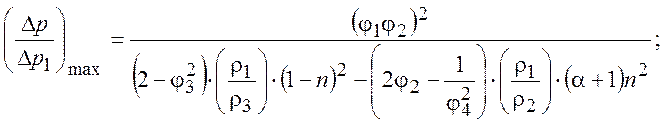 (5)
(5)
![]()
![]()
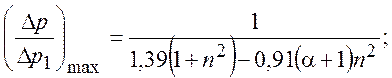 (5')
(5')
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.