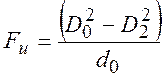
Недостаток: узкий кольцевой зазор, что приводит к ограничению по размеру частиц в рабочей среде во избежание его засорения.
ВКР можно выполнить цилиндрической конструкцией, сделав более одного канала питания и управления. Для макроклапанов нежелательно иметь более 1 - го канала питания, управления и выходного канала. Если размеры клапана порядка нескольких десятков мм, то каналы выполняются механической обработкой (сверление, фрезерование) и их число уже не является большим недостатком. Стремление сделать радиальную конструкцию симметричной при неограниченном увеличении числа каналов, приводит к использованию кольцевого подвода, что несколько усложняет конструкцию.
ПРИЛОЖЕНИЕ
Расчет газового эжектора.
Для указанной схемы на рисунке П1, рассчитать газовый эжектор по следующим параметрам эжектирующего (индекс 01) и эжектируемого (индекс 02) газа.
Температуры торможения.
Давления торможения.
Температуру торможения смеси на выходе Т04 и статическое давление р4.
Для массового расхода m и коэффициента эжекции n найти геометрические размеры и нарисовать схему проточной части.

рис. П1.
![]()
Исходные данные: n=5; m=0.5; T01=900K; T02=300K; T04=400K;
p01=3 105 Па; p02=105 Па; p4=1,05 105 Па;
![]()
где : n-коєффициент эжекции , Т01-температура эжектирующего газа ,
Т02-температура эжектируемого газа , Т04-температура газа на выходе из диффузора ,р01-абсолютное давление эжектирующего газа ,р02- абсолютное давление эжектируемого газа , p4- абсолютное давление газа на выходе из диффузора , m-массовый расход.
![]()
Требуется найти геометрические размеры эжектора удовлетворяющему исходным данным.
![]()
Определим безразмерные параметры.
![]()
Для того , чтобы выяснить
значения ![]() ,необходимо установить режим истечения из
сопла , для этого сравним отношения По и Пкр.
,необходимо установить режим истечения из
сопла , для этого сравним отношения По и Пкр.
Рабочими средами в эжекторе является воздух.
![]()
![]()
Режим истечения из сопла
является сверхкритическим, значит на срезе сопло-скорость, равна скорости звука
(сопло конфузорное). Тогда ![]() на срезе сопла.
на срезе сопла.
Запишем группу газодинамических функций, которые понадобятся нам в расчете:
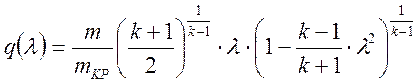 , (1)
, (1)
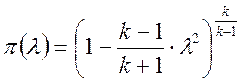 . (2)
. (2)
И обратная зависимость:
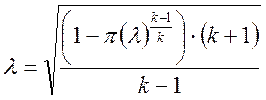 ,
(2.1)
,
(2.1)
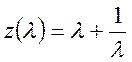 . (3)
. (3)
Для докритического режима:
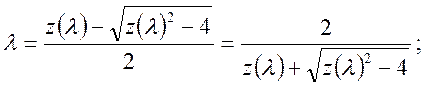 (3.1.1)
(3.1.1)
Для сверхкритического режима:
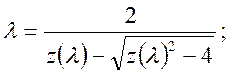 (3.1.2)
(3.1.2)
Из уравнения (1) видно ,что пр l1=1 q(l1)=1 при k=1.4 .
Температура Т03=Т04 для диффузора без учета потерь .
Из уравнения:
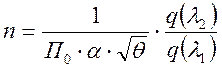 ,
,
найдем геометрический параметр:
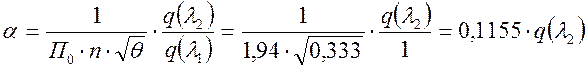 (*)
(*)
Прежде чем строить зависимость ![]() и
и ![]() ,
необходимо выяснить ограничения накладываемые на коэффициент скорости
,
необходимо выяснить ограничения накладываемые на коэффициент скорости ![]() эжектируемого потока во входном сечении камеры смешения.
эжектируемого потока во входном сечении камеры смешения.
Таковыми ограничениями являются:
- 1-е
ограничение вызвано кризисом течения в сечении запирания, т.е. при ![]() :
:
![]() ,найдем
максимально возможное значение
,найдем
максимально возможное значение ![]() из условия
из условия ![]() .
.
Из соотношения ![]() ,определяющего равенство статических
давлений, для
,определяющего равенство статических
давлений, для ![]() :
: 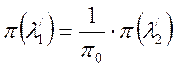 ,
,
найдем ![]() , если
, если ![]() то из
уравнения (2) или из таблицы «газодинамических функций.» (табл. 1) найдем
то из
уравнения (2) или из таблицы «газодинамических функций.» (табл. 1) найдем ![]()
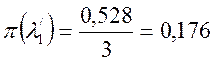 .
.
Из ![]() найдем
значение
найдем
значение ![]() по формуле (2.1) при
по формуле (2.1) при ![]() или из таблицы 1 (см. приложение).
или из таблицы 1 (см. приложение).
![]() ,
откуда находим
,
откуда находим ![]() из формулы (1) или табл.
из формулы (1) или табл. ![]() .
.
Из уравнения:
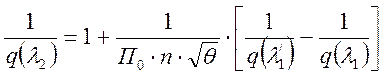 ,
,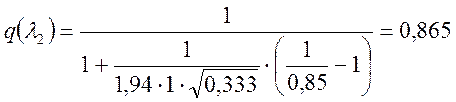
![]() ,
откуда с помощью таблицы 1 находим
,
откуда с помощью таблицы 1 находим ![]() .
.
- 2-е ограничение определяется из условия кризиса течения на выходе из камеры смешения (сечение 3).
![]() .
.
Из основного уравнения эжекции:
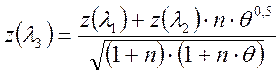 , (4)
, (4)
находим ![]() подставив в уравнение (4)
подставив в уравнение (4) ![]() и
и ![]() при
при ![]() и
и ![]() из уравнения (3)
из уравнения (3) ![]() и
и ![]() .
.
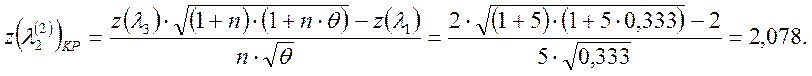
Из ![]() находим
находим
![]() по формуле (3.1.1)- для докритического режима
по формуле (3.1.1)- для докритического режима
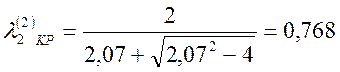 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.