Зная два ограничения для ![]() выбираем с наименьшим значением
выбираем с наименьшим значением ![]() , следовательно Э будет работать в
критическом (наивыгоднейшем) режиме:
, следовательно Э будет работать в
критическом (наивыгоднейшем) режиме:
![]() и
и 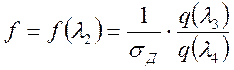 , где
, где 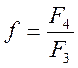
![]() и
и ![]() выбираем
выбираем ![]() .
.
Задаваясь значениями ![]() строим
функции
строим
функции ![]() и
и ![]() .
Таблица Зависимость геометрических комплексов a и f от коэффициента скорости l2.
.
Таблица Зависимость геометрических комплексов a и f от коэффициента скорости l2.
|
l2 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.725 |
|
|
0.3102 |
0.4227 |
0.5897 |
0.7091 |
0.8109 |
0.8924 |
0.91 |
|
|
5.2 |
3.63 |
2.9 |
2.5 |
2.266 |
2.128 |
2.104 |
|
|
0.0358 |
0.0526 |
0.0681 |
0.0819 |
0.0937 |
0.104 |
0.105 |
|
|
4.25 |
3.12 |
2.59 |
2.3 |
2.138 |
2.037 |
2.0 |
|
|
0.25 |
0.363 |
0.472 |
0.582 |
0.691 |
0.825 |
1 |
|
|
0.3842 |
0.54 |
0.679 |
0.795 |
0.886 |
0.962 |
1 |
|
|
0.964 |
0.924 |
0.875 |
0.815 |
0.746 |
0.656 |
0.5283 |
|
|
0.982 |
0.965 |
0.951 |
0.938 |
0.924 |
0.912 |
0.9 |
|
|
0.18 |
0.25 |
0.29 |
0.33 |
0.365 |
0.395 |
0.43 |
|
|
0.2801 |
0.384 |
0.4416 |
0.4472 |
0.547 |
0.580 |
0.6272 |
|
|
1.4 |
1.48 |
1.57 |
1.63 |
1.65 |
1.69 |
1.7 |
Задаваясь значениями ![]() по формуле (1) или таблице 1 определяем
по формуле (1) или таблице 1 определяем ![]() , из уравнения (*) определяем
, из уравнения (*) определяем ![]() . Подставляя значение
. Подставляя значение ![]() и
и ![]() в
уравнение (4):
в
уравнение (4):
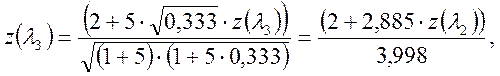
![]() находим
из уравнения (3-1). Далее по формуле (1) и (2) или табл. 1 находим
находим
из уравнения (3-1). Далее по формуле (1) и (2) или табл. 1 находим ![]() и
и ![]() :
:
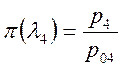 ,
,
где ![]() , (
, (![]() )
)
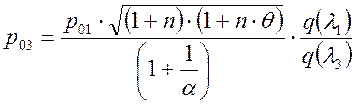 .
.
Из уравнений следует, что:
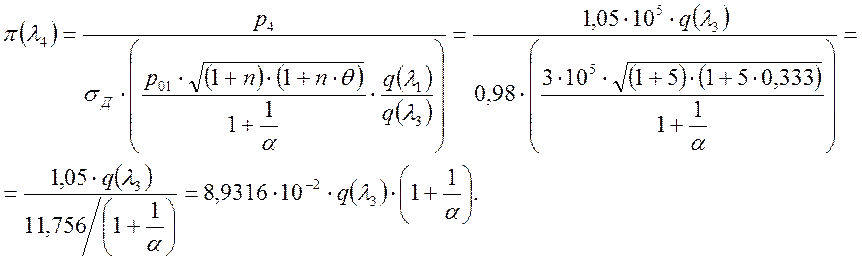
Из ![]() находим
находим
![]() по формуле (2.1) и (1) или таблице:
по формуле (2.1) и (1) или таблице:
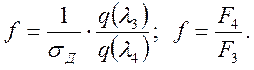
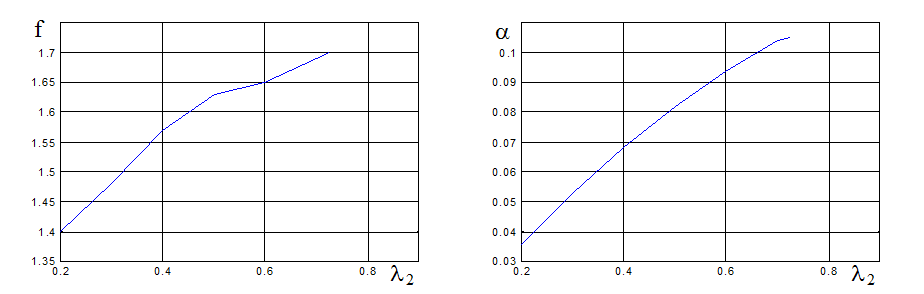 |
рис. П1 рис. П2
На рис. П1 и П2
представлены геометрические параметры эжекторов ![]() и
и ![]() в зависимости от
в зависимости от ![]() .
.
Задача решения в
относительных параметрах , для перехода к относительным геометрическим
параметрам необходимо задать ![]() и
и ![]() либо один из абсолютных геометрических
параметров
либо один из абсолютных геометрических
параметров ![]() .
.
При заданном ![]() геометрические размеры находятся по
формулам:
геометрические размеры находятся по
формулам:
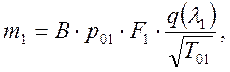 ,
,
где 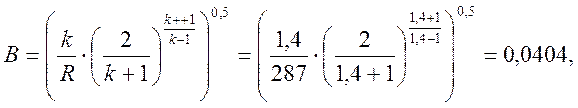
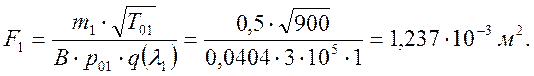
Из расчетного диапазона от ![]() можно выбирать любую пару значений
a и f.
можно выбирать любую пару значений
a и f.
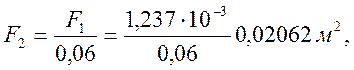
![]()
![]()
Находим диаметры:
![]()
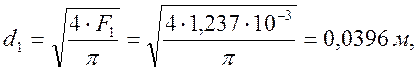
![]()
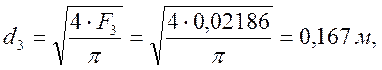
![]()
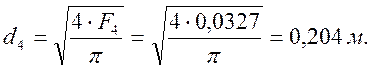
![]() Длина камеры смешения:
Длина камеры смешения:
![]()
![]()
Длина диффузора при угле ![]() :
:
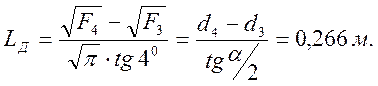
По рассчитанным значениям получаем схему проточной части (рис. П3).
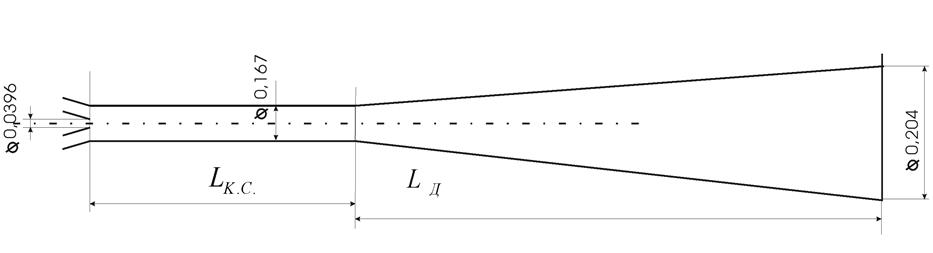
Рис. П3. Схема проточной части эжектора.
Таблица газодинамических функций
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.