Другие предметы \ Струйная техника

Струйные аппараты. Основные элементы конструкций струйных аппаратов поступательного движения. Общие сведения из теории свободных турбулентных струй. Основные уравнения газового эжектора. Струйные насосы. Струйные вихревые элементы, страница 6


n = 0,2
 

А
 
 Рассчитанные таким образом характеристики представлены на рис. 12.         

a = 0,5
 

n = 0,3
 

p03/p02
 
 


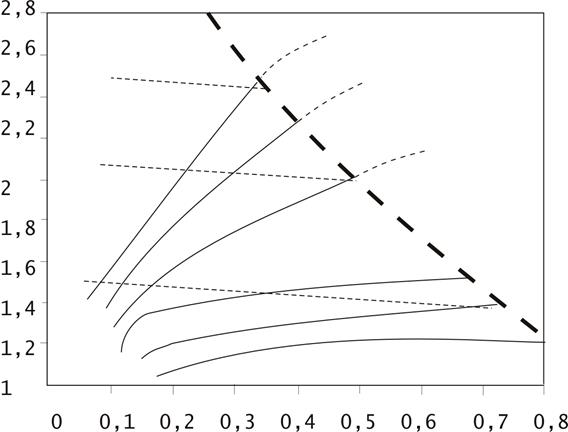
Рис. 12 Зависимость степени повышения полного давления в эжекторе от коэффициента эжекции (n) и коэффициента скорости  эжектируемого потока при фиксированных По, ,  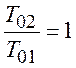для воздуха А–Б – линия максимально возможных значений λ2.

Из рисунка 12 следует:

1)  полное давление смеси газов растёт с уменьшением коэффициента эжекции, однако при этом энергия, приходящаяся на единицу расхода эжектируемого газа растёт;

2)  при заданном  фиксированном   коэффициенте эжекции n полное давление возрастает с увеличением начальной скорости  эжектируемого газа, т. к. снижаются потери на удар, которые пропорциональны разнице квадратов скоростей эжектирующего и эжектируемого потоков.

3)  При различных значениях коэффициента скорости эжектируемого потока  и фиксированного коэффициента эжекции следует брать разные значения геометрического параметра , это значит, что точки на кривых  относятся к разным  эжекторам, имеющим разные значения , при этом, чем больше  , тем меньше должна быть относительная площадь камеры смешения, что соответствует большим значениям .

Примечание: при выборе коэффициентов и , следует учитывать, что они не являются взаимно независимыми, а условия, определяющие их взаимосвязь, зависят от того дозвуковыми или сверхзвуковыми являются потоки; условия взаимосвязи  и ограничивают области  возможных  скоростей смешивающихся потоков.

Рассмотрим случай, когда эжектирующий и эжектируемый потоки являются дозвуковыми: , .

При дозвуковом истечении статическое давление во  входном  сечении камеры смешения постоянно, т. е. статические давления эжектирующего  и эжектируемого потоков одинаковы .

Используя газодинамическую функцию давления

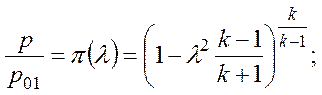
равенство статических давлений можно представить в виде:

или

 

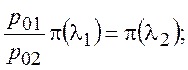
Обозначим                                           .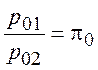

Тогда

,                                                 (1)

Условие (1) связывает между собой значения  коэффициентов скорости  и  при дозвуковом истечении. Только один из коэффициентов скорости может быть задан произвольно, а значение второго  должно быть задано с использованием условия (1). Для каждого  По можно брать такое значение , которое соответствует значениям, , при этом:

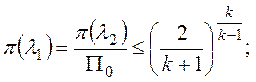
При сверхзвуковом истечении эжектирующего потока соотношение (1) использовать нельзя, т. к. при этом не соблюдается равенство статических давлений  и .

7. ОСОБЕННОСТЬ ИСТЕЧЕНИЯ ИЗ СУЖИВАЮЩЕГОСЯ СОПЛА ЭЖЕКТОРА ПРИ СВЕРХКРИТИЧЕСКИХ ОТНОШЕНИЯХ ДАВЛЕНИЙ

Так как сопло суживающееся, то даже при сверхкритических отношениях давлений 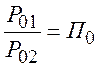, на его выходе устанавливается критическая скорость равная скорости звука.

Кроме того; т.е. – газ, вытекая из сопла в камеру смешения, продолжает расширяться (см. Рис. 12). При этом на участке расширения эжектирующие и эжектируемые потоки практически не смешиваются между собой.

 Эжектирующий газ, вытекая со звуковой скоростью и расширяясь, приобретает скорость большую, чем скорость звука.

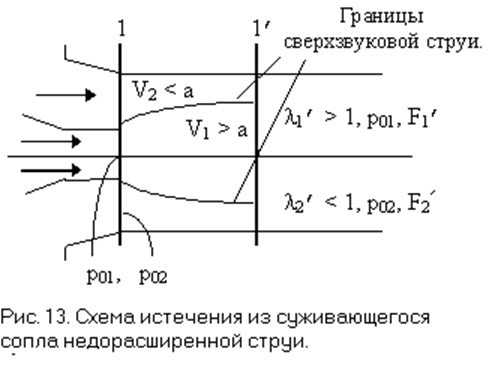
При возможности газ будет расширяться до давления равного давлению эжектируюемого газа. Поток эжектируемого газа движется к сечение 1' – 1' в конфузном (суживающемся) канале, образованном стенками камеры смешения и границами сверхзвуковой эжекторной струи. Смешение струй при этом незначительно. Т. к. площадь поперечного сечения   канала  для  эжектируемой струи уменьшается то скорость ее растет, а давление падает.

Скачать файл