Как было указано выше, заданными в расчёте считаются параметры смеси эжектирующего и эжектируемого газа, камера смешения цилиндрическая.
Необходимо найти параметры смеси эжектирующего и эжектируемого газов.
Дано:
![]() ,
, ![]()
![]() .
.
Найти:
![]()
1. Из уравнения сохранения массового расхода:
![]()
Запишем баланс расходов:
![]()
или в относительном виде:
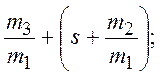
Введем обозначение:
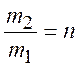 – коэффициент эжекции,
– коэффициент эжекции,
тогда
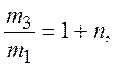 (1)
(1)
2. Из уравнения сохранения энергии:
![]()
![]()
![]()
где ![]() -
секундное количество тепловой энергии подведенное (отведенное) к (от) одного
кг массы смеси между сечениями 1 – 3 за счёт теплообмена, преобразования работы
трения в тепло, возможно, также горение или термическая реакция при
взаимодействии потоков с охлаждением.
-
секундное количество тепловой энергии подведенное (отведенное) к (от) одного
кг массы смеси между сечениями 1 – 3 за счёт теплообмена, преобразования работы
трения в тепло, возможно, также горение или термическая реакция при
взаимодействии потоков с охлаждением.
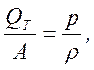
где ![]() –
тепловой эквивалент механической работы.
–
тепловой эквивалент механической работы.
![]()
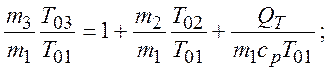
Введем
обозначения: 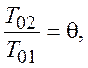
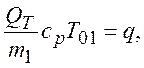 учитывая
уравнение (1), получим:
учитывая
уравнение (1), получим:
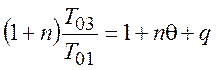
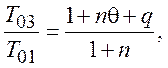 (2)
(2)
Предположим,
что ![]() невелико
невелико ![]() , тогда:
, тогда:
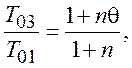 (3)
(3)
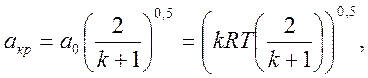
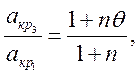 (4)
(4)
Считаем,
что ![]() – показатель адиабаты, для газовой смеси
везде одинаков. Для определения скорости составим уравнение количества движения
для потока в канале смешения (см. рис.10):
– показатель адиабаты, для газовой смеси
везде одинаков. Для определения скорости составим уравнение количества движения
для потока в канале смешения (см. рис.10):
![]()
![]()
![]()
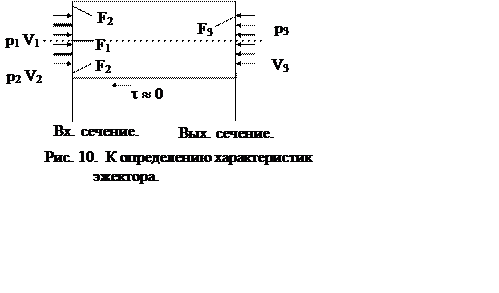
![]()
Это же выражение запишем через импульс, припоминая, что его величина определяется как
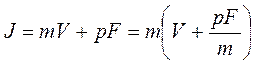 .
.
Тогда
![]() (**)
(**)
Придадим выражению для импульса иной вид.
С учетом известных и ранее введенных отношений:
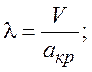
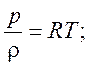
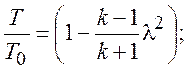
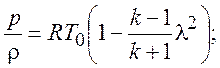
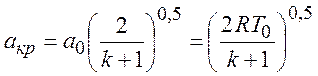 (*)
(*)
После подстановки в выражение для импульса
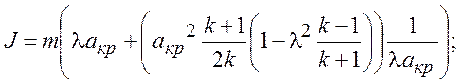
и тождественных преобразований
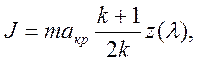 (5)
(5)
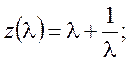
Полученное
выражение для импульса (5), используем для записи уравнения сохранения
импульсов (**), по-прежнему считая ![]() - неизменным для газов
и смеси, т.е.
- неизменным для газов
и смеси, т.е. ![]() ~ idem или (
~ idem или (![]() =
=![]() =
=![]() ). Тогда после подстановки (5) в (**) получим:
). Тогда после подстановки (5) в (**) получим:
![]()
или
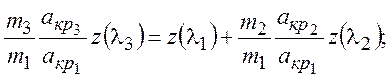
С учетом ранее полученных отношений:
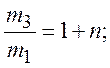
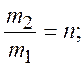
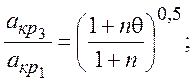
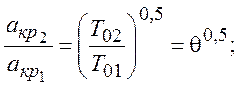
после их подстановки в последнее уравнение, будем иметь:
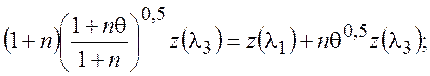
и окончательно:
![]() . (6)
. (6)
Уравнение (6) – основное уравнение эжекции, которое позволяет найти скорость в выходном сечении смесительной камеры.
Зная
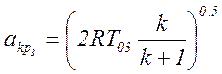 находим
находим ![]() более
того, зная
более
того, зная ![]() определим
определим
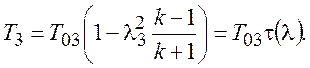 Итак, два параметра потока на выходе из
смесительной камеры найдены – это
Итак, два параметра потока на выходе из
смесительной камеры найдены – это ![]() и
и ![]() .
.
Найдем
![]() :
:
![]()
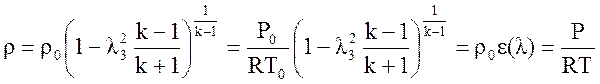
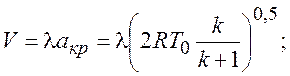
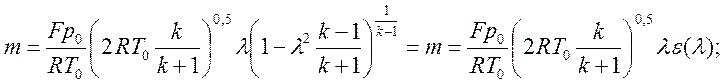
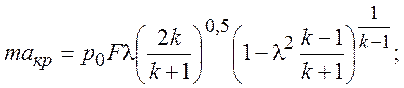
Введем дополнительную газодинамическую функцию, именуемую расходной, (график приведен на рис.11):
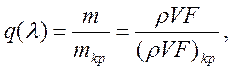
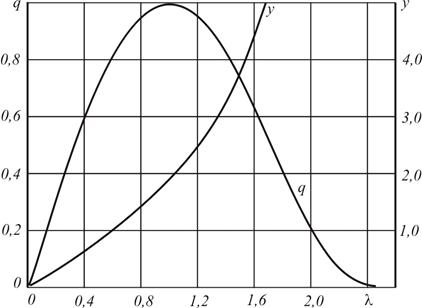
Ее выражение через коэффициент скорости получим так:
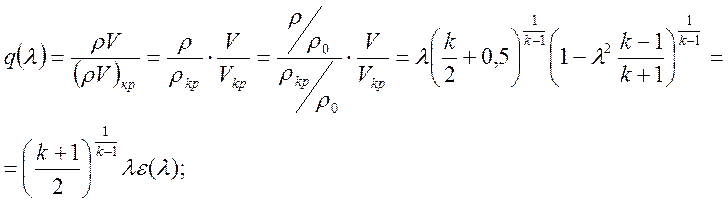
С учетом этой функции, будем иметь:
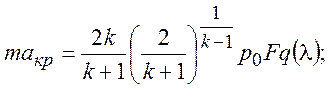
или
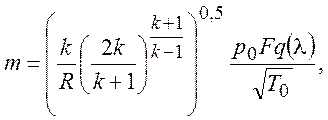 (7)
(7)
После замены в уравнении неразрывности (1) m3 и m1, с использованием полученного выражения массового расхода через газодинамическую функцию q(l), будем иметь:
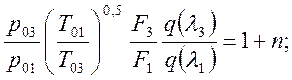
По-прежнему
считаем, что ![]() и
и ![]() –idem,
упростив полученное выражение, с учетом принятых ранее допущений, а также
уравнения (3), получим:
–idem,
упростив полученное выражение, с учетом принятых ранее допущений, а также
уравнения (3), получим:
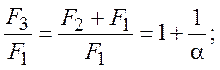
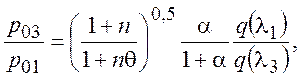 (8)
(8)
Зная Р03 из (8) находим статическое давление на выходе из камеры смешения:
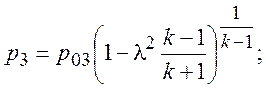
Таким
образом, если заданы параметры торможения ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , соответственно для
эжектирующего и эжектируемого потоков, а также коэффициент эжекции
, соответственно для
эжектирующего и эжектируемого потоков, а также коэффициент эжекции 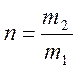 или
или 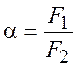 , то на
основе выражений (3), (4), (6) и (8) могут быть определены параметры смеси в
конечном сечении камеры смешения.
, то на
основе выражений (3), (4), (6) и (8) могут быть определены параметры смеси в
конечном сечении камеры смешения.
Статические давления Р1 и Р2 в начале расчёта неизвестны т. к. зависят от режима работы эжектора и эффективности камеры смешения и диффузора. Поэтому сначала расчета задаются значениями l1 и l2, затем, производя расчет по блок-схеме, строят сетку характеристик работы эжектора, из которой определяется наилучший или требуемый режим.
Лекция№4
6. БЛОК -СХЕМА РАСЧЕТА ЭЖЕКТОРА.
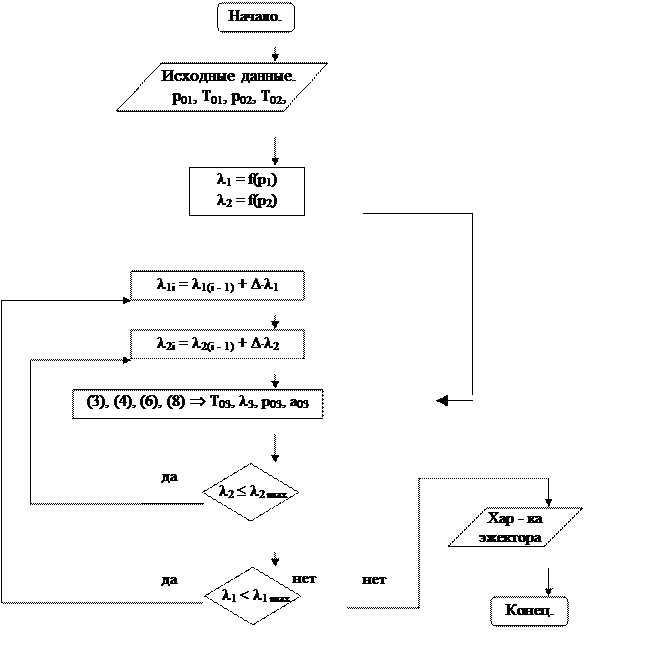 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.