Струйные аппараты. Основные элементы конструкций струйных аппаратов поступательного движения. Общие сведения из теории свободных турбулентных струй. Основные уравнения газового эжектора. Струйные насосы. Струйные вихревые элементы, страница 4

Интегрируя обыкновенное линейное дифференциальное уравнение третьего порядка (7), получим интеграл в форме

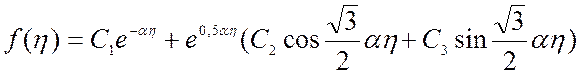                (10).

который описывает распределение скорости в  каждом из сечений и где , представляет единственную эмпирическую константу.

Коэффициенты C₁, C₂, C₃ и корни уравнения определяются из условия плавности перехода скоростей из невозмущенной области в область пограничного слоя:

,  ,  ,  ,  

Решение уравнения  (10) даёт:

С₁ = 0,0062;          С₂ = 0,987;   С₃ = 0,577;    ah₁ = 0,981;   ah₂ =  - 2,04

ah

По экспериментальным данным, полученным в  лаборатории Прандтля:

;; .

Vx/V0

a×Vy/V0

При течении реальных турбулентных струй сопла имеют конечные размеры,  твёрдые границы находятся не на бесконечности и оказывают влияние  на распространение струй. С учётом  реальных  граничных условий решение задач распространения струи  усложняется  и  как  пра-

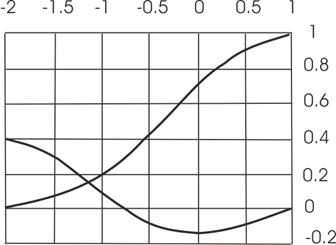
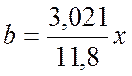вило аналитическими методами  решено быть не может.

В этих случаях задачи решают численными методами или опытным путём - на основе физического эксперимента.

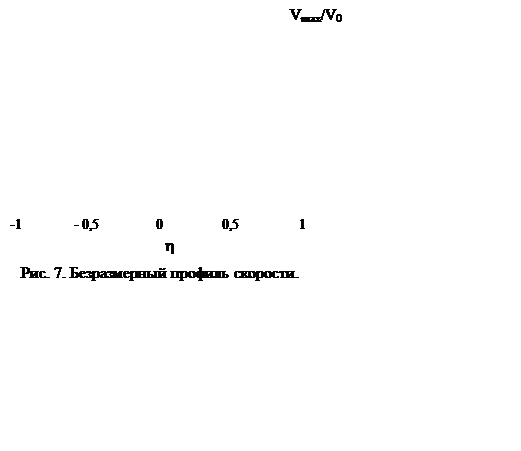
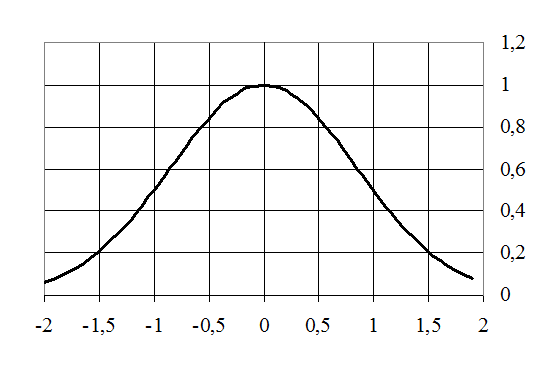
Накопленный опыт измерения параметров истечения турбулентных струй из сопел конечных размеров различной формы поперечного сечения позволяют установить и принять для инженерной практики следующую упрощённую картину распространения струи прямоугольной и круглой формы, а также установить следующие их параметры.

Рис. 6. К определению параметров затопленной струи

Таблица 1.

Параметры струи.			Круглая струя.	Плоская струя.
Коэффициент структуры струи.
Полюсное расстояние.
Длина начального участка.
Тангенс  угла одностороннего расширения  струи.
Полуширина струи.
Осевая скорость на основном участке.
Закон распределения скорости жидкости поперёк струи.
	Нач.  уч-к.	Круглая струя:             Плоская струя:
	Осн-й. уч-к.	Круглая струя: Плоская струя:

 

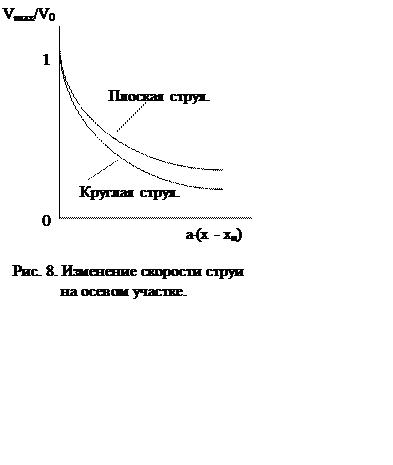Лекция№3

5. ОСНОВНЫЕ УРАВНЕНИЯ ГАЗОВОГО ЭЖЕКТОРА

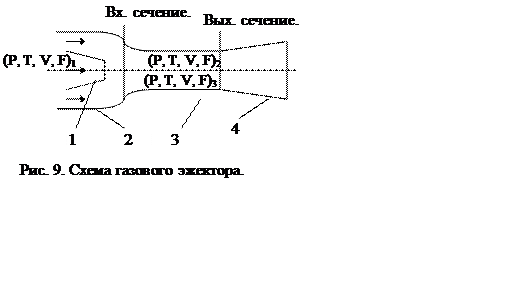                                           1 – рабочее сопло

                                                                                    2 – сопло эжектируемого газа

                                                                                    3 – цилиндрическая смесительная камера круглого сечения.

4 – диффузор (в конструкции не обязателен)

Задачей расчёта эжектора является определение параметров смеси на выходе из смесительной камеры, по заданным параметрам в её входном сечении, т. е. заданы параметры эжектирующего и эжектируемого газа. При этом рассмотрение самого процесса смешения необязательно, нет необходимости анализировать механизм передачи энергии и предварительно вычислять возникающие потери энергии. Для проведения расчётов достаточно трёх уравнений сохранения  - массы, энергии и количества движения, которыми описаны состояние газа на любом участке смесительной камеры.

Как известно, три параметра P, T, S полностью характеризуют состояние потока газа и позволяют найти  все остальные параметры при расчёте. Полагают, что распределение скоростей эжектирующего газа  на выходе из сопла, эжектируемого газа на входе в смесительную камеру и смеси газов на выходе из смесительной камеры, равномерны, т. е.  треугольники скоростей прямоугольны. Использование интегрального подхода приводит к правильному результату независимо от того, какие процессы протекают между начальным и конечным сечениями камеры смешения, т. е. есть ли в ней скачки уплотнения, имеются ли вихри, встречные потоки, насколько интенсивно  перемешаны рабочие и эжектируемые потоки.