Струйные аппараты. Основные элементы конструкций струйных аппаратов поступательного движения. Общие сведения из теории свободных турбулентных струй. Основные уравнения газового эжектора. Струйные насосы. Струйные вихревые элементы, страница 3

В теории пограничного слоя нами были рассмотрены осреднённые уравнения Навье - Стокса, для случая пограничного турбулентного слоя. Пренебрегая в них касательными напряжениями, которые вызваны молекулярной     вязкостью  и учитывая турбулентные напряжения в соответствии   с   гипотезами   Буссинеска   и

 Прандтля, а также считая неизменным статическое давление вдоль и поперёк струи (как в самой струе, так и  в окружающей среде), вместе с уравнением неразрывности уравнения движения примут вид:

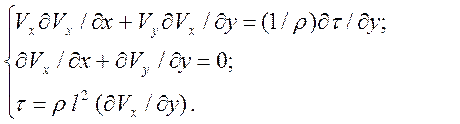                                (1)

В последнем уравнении системы (1), т.е. гипотезе Прандтля, масштаб турбулентности  считается величиной постоянной по поперечному сечению - как в гипотезе Буссинеска. Вместе с тем, при переходе от сечения к сечению, эта величина изменяется, как будет показано, линейно - как в гипотезе Прандтля.

Решение системы уравнений  (1) находят, предварительно заменив скорости их выражениями через функцию тока  :

,   .

Подставив данные значения в систему (1), получим:

.       (2)

Запишем  граничные условия, считая течение в невозмущенной части струи плоскопараллельным, а поле скоростей - однородным, имеющим скорость .

Для верхней части струи:

      при          

               ;

      при .                                               (3.1-3.2).

Для нижней части струи:

     при           и

     при         

форма границ струи пока остается неизвестной.

Для определения , введем масштабы длины и функции тока, соответственно, и .

      Из первого граничного условия следует связь между введенными масштабами:

.

Это значит, что решение уравнения (2) в безразмерном виде должно иметь следующий общий вид:

или

.

Но масштаб  отсутствовал в постановке задачи, значит, его не должно быть и в решении. Следовательно, безразмерная функция тока должна быть записана в виде

.

При этом масштаб длин  выпадает, и размерная функция тока будет иметь вид:

.                                              (4)

Обозначив отношение координат точки струи как

,

перепишем уравнение для размерной линии тока:

.

С учетом последнего выражения вычислим все частные производные входящие в уравнение (2):

,  ,  ,

,  .

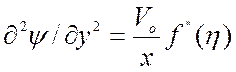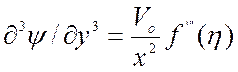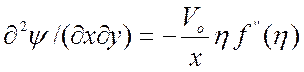Подставляя их в (2), после простых преобразований получим обыкновенное дифференциальное уравнение:

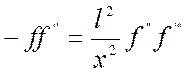,                                                        (5)

где  - функция относительных параметров, следовательно, отношение величин  не должно зависеть от абсолютного значения координаты . А это возможно только в случае, если они линейно связаны, т.е.

,                                                   (6)

где - эмпирическая константа, зависящая от турбулентной структуры пограничного слоя, т.е. от предыстории потока.

Уравнение (5) распадается на два уравнения:

   

и

.                                                     (7)

Первое уравнение соответствует невозмущенному движению в ядре струи, т.е. равенствам (3.1), которые согласно (4), можно теперь переписать в виде:

или

,

откуда

.

Обозначим через  наименьший положительный корень последнего уравнения и через  наименьший по абсолютной величине отрицательный корень уравнения .

Тогда, с учетом принятого обозначения корней, уравнение верхней границы струи, из граничных условий (3.1) будет таким:

или

.

Уравнение нижней границы, соответственно:

.

Таким образом, границы пограничного слоя смешения струи с окружающей ее жидкостью тех же физических свойств, представляют прямые линии на плоскости.

Между границами  находится  струйный  пограничный  слой,  ширина  которого

,                                                   (9)

пропорциональна продольной координате. Сравнивая полученное соотношение с формулой (6) для масштаба турбулентности, заключаем, что принятое предположение постоянства   в данном сечении, эквивалентно допущению о пропорциональности пути смешения ширине струи.

         Так как постоянная  зависит от предыстории потока, гипотеза Прандтля уже перестает носить локальный характер и речь уже идет о смешении интегрального и дифференциального подходов.