Система лінійних диференціальних рівнянь у скалярній формі має вигляд:
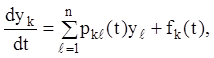 (k = 1,2,…,n),
(2...67)
(k = 1,2,…,n),
(2...67)
де ![]() й
й
![]() (k = 1,2,…,n) є неперервними функціями
дійсного змінного на t(a, b). Якщо ввести матрицю коефіцієнтів P(t) порядку n´n й n-мірні вектори
(k = 1,2,…,n) є неперервними функціями
дійсного змінного на t(a, b). Якщо ввести матрицю коефіцієнтів P(t) порядку n´n й n-мірні вектори ![]() й
й ![]() :
:
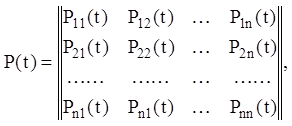
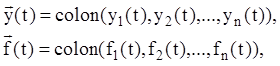 (2.68)
(2.68)
то система (2.66) запишеться у векторній формі:
 (2.69)
(2.69)
Системи (2.66), (2.68) називаються лінійними неоднорідними системами.
Якщо в системі (2.66) всі ![]() (l = 1,2,…,n), або в
системі (2.68)
(l = 1,2,…,n), або в
системі (2.68) ![]() то ці системи називаються однорідними.
Задача Коші для векторного рівняння (2.68) записується так:
то ці системи називаються однорідними.
Задача Коші для векторного рівняння (2.68) записується так:
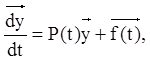 (2.70)
(2.70)
![]() (2.71)
(2.71)
де ![]() –
будь-який заданий n-мірний вектор:
–
будь-який заданий n-мірний вектор:
![]() (2.72)
(2.72)
Розв'язанням задачі (2.70) - (2.71) називається такий n-мірний диференційований вектор
![]() (2.73)
(2.73)
який задовольняє при ![]() рівнянню (2.70) і початковій умові (2.71).
рівнянню (2.70) і початковій умові (2.71).
Розглянемо лінійну однорідну систему:
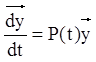 (2.74)
(2.74)
і введемо для неї матрицю
Y(t) порядку n ´ n, складену з n лінійно незалежних розв'язань
рівняння (2.74) ![]() з огляду на що
з огляду на що
![]()
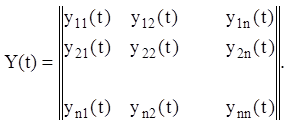 (2.75)
(2.75)
Очевидно, що Y(t) задовольняє матричному рівнянню:
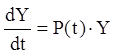 (2.76)
(2.76)
При цьому матрицю (2.74), безупинно диференційовану й неперервну у всіх
точках ![]() яка обертає рівняння (2.75) у тотожність,
називають інтегральною матрицею системи (2.76) або фундаментальною
матрицею цієї ж системи.
яка обертає рівняння (2.75) у тотожність,
називають інтегральною матрицею системи (2.76) або фундаментальною
матрицею цієї ж системи.
Підкреслимо ще раз, що лінійна однорідна система диференціальних рівнянь може бути записана або у векторній формі (2.74) або в матричній формі (2.76). Зв'язок між цими рівняннями полягає в наступному: вирішити матричну систему (2.76) – означає знайти матрицю Y(t) порядку n ´ n, стовпці якої являють собою лінійно незалежні розв'язання векторного рівняння (2.74).
Звернемо увагу й на те, що довільне розв'язання матричного рівняння (2.76) не обов'язково буде його інтегральною матрицею. Це буде у випадку, якщо на стовпці матриці Y не будуть накладатися обмеження лінійної незалежності.
Нехай задана лінійна однорідна система рівнянь загального виду:
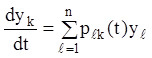 (k =
1,2,…,n), (2...77)
(k =
1,2,…,n), (2...77)
коефіцієнти якої неперервні
при ![]() Матриця коефіцієнтів системи (2.77)
Матриця коефіцієнтів системи (2.77)
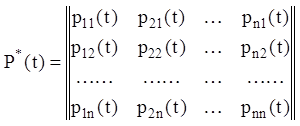 (2.78)
(2.78)
є очевидно транспонованою матрицею стосовно матриці (2.68) системи (2.67). Зміна порядку індексів у коефіцієнтів розглянутої системи (2.76) у порівнянні із системою (2.66) пояснюється зручністю подальших викладень при використанні раніше викладених понять теорії лінійних систем диференціальних рівнянь.
Нехай система рівнянь (2.77) має фундаментальну систему розв'язань:
![]() (i =
1,2,…,n)... (2.79)
(i =
1,2,…,n)... (2.79)
При послідовній підстановці розв'язань (2.79) у систему рівнянь (2.77)
одержимо ![]() тотожностей:
тотожностей:
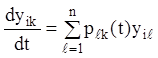 (i, k =1,2,…,n; tÎ (a, b))... (2.80)
(i, k =1,2,…,n; tÎ (a, b))... (2.80)
З огляду на (2.79), введемо матрицю фундаментальної системи розв'язань:
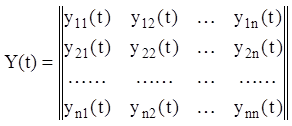 (2.81)
(2.81)
Тоді систему ![]() тотожностей (2.80) можна записати
у вигляді однієї матричної тотожності. Справді:
тотожностей (2.80) можна записати
у вигляді однієї матричної тотожності. Справді:
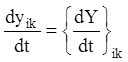 ,
(2.81’)
,
(2.81’)
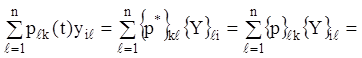
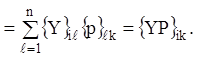 (2.82)
(2.82)
З урахуванням (2.81), (2.82) тотожності (2.80) приймають вид:
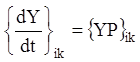 (i, k =1,2,…,n; tÎ (a, b)),
(i, k =1,2,…,n; tÎ (a, b)),
що еквівалентно матричній тотожності:
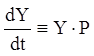 (a < t < b). (2.83)
(a < t < b). (2.83)
Таким чином, матриця фундаментальної системи розв'язань (2.80) є розв'язанням матричного рівняння
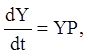 (2.84)
(2.84)
відповідній заданій системі рівнянь (2.79).
Слід зазначити, що матричне рівняння (2.84) еквівалентно матричному рівнянню (2.76). Для доказу цього досить зробити транспонування матриць у рівності (2.84), використовуючи формулу (2.23). Однак форма матричного рівняння (2.84) більш зручна при практичному застосуванні розглянутого методу. У цьому випадку матриця фундаментальної системи розв'язань така, що окремі розв'язання розташовуються по рядках, а не по стовпцях, як у випадку (2.76).
Значення інтегральної матриці Y у точці ![]() називається
початковим її значенням і позначається:
називається
початковим її значенням і позначається:
![]()
![]() (2.85)
(2.85)
Якщо ![]() , то відповідна інтегральна матриця Y
називається нормованої в точці
, то відповідна інтегральна матриця Y
називається нормованої в точці ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.