Матричний метод розв'язання однорідних лінійних систем з постійними коефіцієнтами, страница 3

Якщо покласти то інтегральна матриця, нормована в точці, має вигляд:

                                                                  (2.95)

Тоді, відповідно до другої властивості інтегральних матриць, всі інтегральні матриці рівняння (2.93) виражаються формулою:

                                                                (2.96)

де C - довільна постійна невироджена матриця.

Аналогічний результат можна одержати, використовуючи матричні ряди й для рівняння

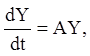                                                               (2.97)

де A - постійна матриця коефіцієнтів лінійної однорідної системи, Y(t) - шукана фундаментальна матриця порядку n стовпці якої є лінійно незалежними розв'язаннями векторного рівняння:

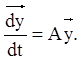
Поставимо задачу знаходження частинного рішення матричного рівняння (2.97), що задовольняє заданим початковим умовам:

                                                       (2.98)

де – задана постійна невироджена матриця порядку n. Розкладемо шукане розв'язання Y(t) у ряд Маклорена по степені t:

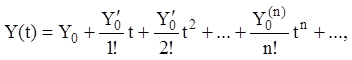                                  (2.99)

де  .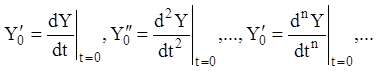

З (2.97) диференціюванням знаходимо:

                     (2. 100)

Підставляючи в (2.100) значення t = 0, одержимо:

Тепер ряд (2.99) запишеться:

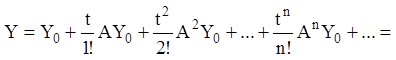
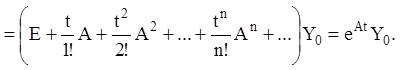
Таким чином, частинне рівняння (2.97), що задовольняє заданим початковим умовам (2.98) має вигляд:

Розглянемо структуру фундаментальної системи розв'язань лінійної однорідної системи диференціальних рівнянь із постійними коефіцієнтами.

Нехай маємо лінійну однорідну систему (2.77):

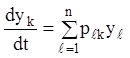  (k = 1,2,…,n),                                 (2...101)

де – дійсну постійну, утворюючу матрицю коефіцієнтів – транспонована стосовно матриці  

Системі (2.77) відповідає матричне рівняння (2.84):

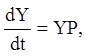                                                      (2. 102)

де P - транспонована матриця коефіцієнтів системи, а Y - матриця фундаментальної системи її розв'язань виду (2.81).

Як відомо, інтегральна матриця має вигляд (2.95):

                                                  (2. 103)

З'ясуємо структуру інтегральної матриці залежно від матриці коефіцієнтів P і покажемо, що структура інтегральної матриці (2.103) повністю визначається елементарними дільниками матриці P, тобто структурою цих дільників.

1. Нехай матриця P має прості елементарні дільники:

                                             (2. 104)

причому серед характеристичних чисел матриці P можуть бути й рівні (не виключається наявність кратних характеристичних чисел). У цьому випадку, згідно (2.42), матриця P перетворення подоби приводиться до канонічного виду в діагональній формі, тобто:

Звідси інтегральна матриця:

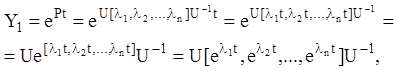                           (2. 105)

при виводі виразу якої використані властивості (2.59), (2.57). Помноживши (2.105) ліворуч на , одержуємо відповідно до  (2.87) інтегрального (уже не нормовану в точці t = 0) матрицю:

                                       (2. 106)

Покладемо, що побудована неособлива матриця має вигляд:

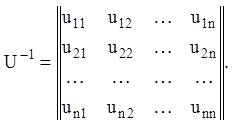                                               (2. 107)

Тоді:

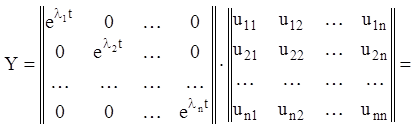
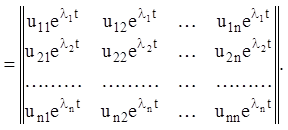                                      (2. 108)

Отриманий вид інтегральної матриці (2.108) визначає структуру фундаментальної системи розв'язань (2.101) для випадку простих елементарних дільників матриці P. У цьому випадку, незалежно від того, чи є характеристичні числа матриці P простими або серед них є кратні, фундаментальна система розв'язань має однакову структуру й складається з розв'язань у вигляді експонентних функцій з деякими постійними множниками. При цьому комплексним характеристичним числам (попарно сполученим для речовинної матриці P) будуть відповідати комплексні (попарно сполучені) рішення, але їх можна замінити дійсними розв'язаннями, визначаючи дійсну й мниму частини в одному (кожному) з розглянутої пари комплексно-комплексно-сполучених розв'язань. Таким чином, завжди можна одержати фундаментальну систему розв'язань, що складає з дійсних функцій.